A soma de dois números quadrados perfeitos revelam interessantes conexões matemáticas com os próprios números quadrados perfeitos, bem como, com números primos, números triangulares, o número 4 e ternos pitagóricos primitivos.
Através da soma de dois números quadrados perfeitos é possível de se gerar uma outra sequência de Ternos Pitagóricos Primitivos que são os Ternos Pitágoricos Primitivos Raros.
Veja matéria relacionadas (abaixo).
Várias são as situações e aplicações em que se utiliza Equação do Segundo Grau ou Equação Quadrática, conhecida por nós brasileiros como Fórmula de Bháskara.
Vários conceitos matemáticos e algébricos são utilizados como: números inteiros, números positivos, números negativos, números racionais, números irracionais, radiciação, coeficientes positivos, coeficientes negativos, etc. quando se resolve Equação do Segundo Grau.
Neste estudo são apresentados exemplos de Equações do Segundo relacionadas a soma de dois números quadrados perfeitos consecutivos e números primos.
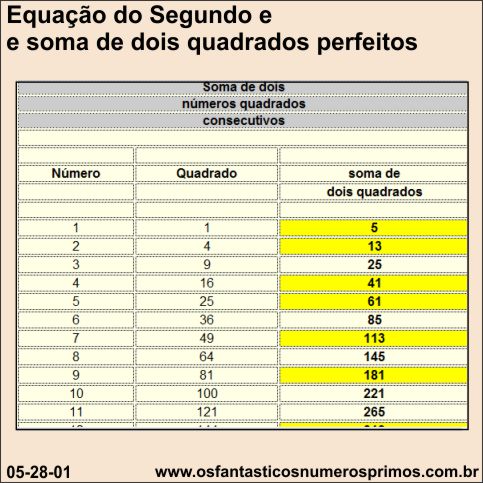
A seguinte tabela apresenta as 20 primeiras somas de dois números quadrados perfeitos consecutivos com os quais se podem extrair as seguintes regularidades numéricas:
a) os algarismos finais das somas possuem o seguinte padrão: 5, 3, 5, 1, 1;
b) 5, é o único número primo terminado em 5;
c) as somas têm como resultados números ímpares, e entre eles, números primos (cor amarelo);
d) das 20 somas, 10 são números primos (50%); resultado bastante interessante, em se tratando de números primos;
e) determinados números primos não podem ser gerados por meio da soma de dois números quadrados perfeitos consecutivos, como: 7, 11, 17, 19, 23, 29, 31, etc...
| Soma de dois | |||
|---|---|---|---|
| números quadrados | |||
| consecutivos | |||
| Número | Quadrado | Quadrado | soma de |
| dois quadrados | |||
| 1 | 1 | 4 | 5 |
| 2 | 4 | 9 | 13 |
| 3 | 9 | 16 | 25 |
| 4 | 16 | 25 | 41 |
| 5 | 25 | 36 | 61 |
| 6 | 36 | 49 | 85 |
| 7 | 49 | 64 | 113 |
| 8 | 64 | 81 | 145 |
| 9 | 81 | 100 | 181 |
| 10 | 100 | 121 | 221 |
| 11 | 121 | 144 | 265 |
| 12 | 144 | 169 | 313 |
| 13 | 169 | 196 | 365 |
| 14 | 196 | 225 | 421 |
| 15 | 225 | 256 | 481 |
| 16 | 256 | 289 | 545 |
| 17 | 289 | 324 | 613 |
| 18 | 324 | 361 | 685 |
| 19 | 361 | 400 | 761 |
| 20 | 400 | 441 | 841 |
| www.osfantasticosnumerosprimos.com.br | |||
A soma dos quadrados de dois números naturais consecutivos é 61. Determine os dois números?
Este problema aparece publicado na página 35, Sequência 6, exercício g, no Livro Nos Domínios da Matemática - autores: José Rui Giovanni e J. Timoni - Editora Ática, 1985.
É um problema bastante interessante, pois, da mesma forma que podemos somar dois números quadrados perfeitos e ter a resposta de tal número, com a Equação do Segundo Grau, temos a tal soma, e precisamos saber quais são as duas raízes geradoras dos números quadrados perfeitos.
As perguntas que não querem calar:
Qual é a chance de se escolher aleatoriamente um número ímpar, que é primo, e ao mesmo tempo ser a soma de dois números quadrados perfeitos?
Qual é a chance de se escolher aleatoriamente dois número quadrados consecutivos, somá-los, e ter como resultado um outro número quadrados perfeito?
x2 + (x + 1)2 = 61
x2 + x2 + 2. x .1 + 12 = 61
2x2 + 2 x + 12 = 61
2x2 + 2 x + 1 - 61 = 0
2x2 + 2 x - 60 = 0 (dividindo por 2)
1x2 + 1 x - 30 = 0
Coeficientes:
a =1
b = +1
c = -30
| - b ± √b 2 - 4 . a .c | ||
| x | = | _____________ |
| 2.a |
| Δ = b2 - 4 . a . c |
i)
| Δ = 12 - 4 . 1 . (-30) |
ii)
| Δ = 1 + 120 |
iii)
O Delta é positivo e maior que 0 (zero), portanto há duas soluções para a equação.
| Δ = 121 |
iv)
| -(+1) ± √121 | ||
| x | = | _____________ |
| 2 |
v)
Raízes da equação
| -1 + 11 | ||||
| x' | = | _____ | = | 5 |
| 2 |
| -1 - 11 | ||||
| x" | = | _____ | = | - 6 |
| 2 |
vi)
verificando a soma de 2 quadrados consecutivos
5 2 = 25
(-6)2 = 36
25 + 36 = 61
Portanto o número 61 que é primo pode ser gerado pela soma de dois números quadrados perfeitos.
Façamos de conta que escolhemos aleatoriamente o número ímpar 11, e desejamos saber se ele é a soma de dois números quadrados consecutivos:
x2 + (x + 1)2 = 11
x2 + x2 + 2. x .1 + 12 =11
2x2 + 2 x + 12 = 11
2x2 + 2 x + 1 - 11 = 0
2x2 + 2 x - 10 = 0 (dividindo por 2)
1x2 + 1 x - 5 = 0
Coeficientes:
a =1
b = +1
c = -5
| - b ± √b 2 - 4 . a .c | ||
| x | = | _____________ |
| 2.a |
| Δ = b2 - 4 . a . c |
i)
| Δ = 12 - 4 . 1 . (-5) |
ii)
| Δ = 1 + 20 |
iii)
| Δ = 21 |
O Delta é positivo e maior que 0 (zero), portanto há duas soluções para a equação.
O Delta não é um número quadrado perfeito.
iv)
| - (+1) ± √21 | ||
| x | = | _____________ |
| 2 |
v)
| - 1 ± √21 | ||
| x | = | _____________ |
| 2 |
Mesmo o Delta não sendo um quadrado perfeito, a solução da equação possui raízes de números irracionais, sendo uma positiva e outra negativa, neste caso, podemos deixar os radicais indicados...
vi)
| - 1 + √21 | ||
| x' | = | _____________ |
| 2 |
vii)
| - 1 - √21 | ||
| x'' | = | _____________ |
| 2 |
... ou verificar quais são as duas raízes irracionais em números decimais.
viii)
| - 1 + 4,582 | ||||
| x' | = | _____________ | = | 1,791 |
| 2 |
ix)
| - 1 - 4,582 | ||||
| x' | = | _____________ | = | 2,791 |
| 2 |
1,7912 = 3,207681...
2,7912 = 7,789681...
3,207681 + 7,789681 = 10,997362...
Portanto o número 11, não pode ser gerado pela soma de dois números quadrados perfeitos.
x2 + (x + 1)2 = 11
x2 + x2 + 2. x .1 + 12 =11
2x2 + 2 x + 12 = 11
2x2 + 2 x + 1 - 11 = 0
2x2 + 2 x - 10 = 0 (dividindo por 2)
1x2 + 1 x - 5 = 0
i)
desloca-se o termo independente "c" 2 para o segundo membro.
x2 + x - 5 = 0
x2 + x = 5
ii)
dividi-se o coeficiente 1 do termo "bx" por 2 e eleve-o ao quadrado, (1/2)2 somando-o ao primeiro e segundo membro.
| 12 | 12 | ||||||||
| x2 | + | x | + | ____ | = | 5 | + | ___ | |
| 22 | 22 |
| 1 | 1 | ||||||||
| x2 | + | x | + | ____ | = | 5 | + | ___ | |
| 4 | 4 |
iii)
efetua-se o Mínimo Múltiplo Comum para se obter frações equivalentes...
| x2 | x | 1 | 5 | 1 | |||||
| ____ | + | ____ | + | ____ | = | ____ | + | ___ | |
| 4 | 4 | 4 | 4 | 4 |
iv)
... e consequentemente também uma equação equivalente.
4x2 + 4x + 1 = 20 + 1
v)
fatora-se o primeiro membro...
4x2 - 4x + 1 = 21
vi)
... obtendo o quadrado da soma (Produto Notável)
(2x + 1)2 = 21
vii)
extrai-se a raiz quadrada
2x + 1 = ± √21
viii)
| - 1 + √21 | 4,582 | |||||
| x' | = | ______ | = | ___ | = | 1,791 |
| 2 | 2 |
ix)
| - 1 - √21 | 5,582 | |||||
| x' | = | ______ | = | ___ | = | 2,791 |
| 2 | 2 |
Portanto o número 11, não pode ser gerado pela soma de dois números quadrados perfeitos.
Com os exemplos acima, foi possível demonstrar que há números que podem ser a soma de dois quadrados perfeitos e outros não.
Os exemplos acima deixam dois grandes desafios:
1) saber se um número que é soma de dois quadrados perfeitos é um número primo, especialmente números grandes, com muitos algarismos, pois tem-se a etapa de decomposição em fatores primos de um número e que demanda tempo, seja feita de forma manual com lápis e papel ou mesmo utilizando computadores com programas específicos para cálculos matemáticos.
Reparar também que a tabela da soma de dois números quadrados perfeitos, funciona como um filtro, pois os resultados das somas só há números terminados em 5, 3, 5, 1 e 1; retirando-se os de finais 5, ficam os que terminam em 1 e 3, aumentando-se a possibilidade de se encontrar número primo.
2) quantos números quadrados podemos encontrar por meio da soma de dois números quadrados perfeitos consecutivos?
Autor: Ricardo Silva - setembro /2020
ANDRADE, Bernardino Carneiro de . A evolução histórica da resolução das equações do 2o grau. Departamento de Matemática Pura da Faculdade de Ciências da Universidade do Porto,2000
DANTE, Luiz Roberto . Tudo é Matemática / Luiz Roberto Dante - - 3. ed. - - São Paulo: Àtica, 2009
IEZZI, Gelson. Matêmática e realidade: 90 ano / Gelson Iezzi, Osvaldo Dolce, Antonio Machado. - 6. ed. - São Paulo: Atual, 2009
VALE, Alberton Fagno Albino do. As diferentes Estratégias de Resolução da Equação do Segundo Grau. Dissertação apresentada à Universidade Federal Rural do Semiárido – Ufersa, Mossoró, 2013
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos
FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.
Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato
