capa dos livros: os fantásticos números primos, sequências numéricas mágicas, estudos de sequências númericas, o triângulo retângulo

Página Textos

Equação do Segundo Grau, perímetro e área de retângulo - 029

O retângulo é um quadrilátero que possui dois pares de lados de medidas congruentes e paralelos podendo ser construído com instrumentos de desenho como: lápis, régua, esquadrados, papel quadriculado ou mesmo ser desenhado em suportes de materiais diversos como: papel, lousa, etc., ou ainda em softwares de desenho, softwares de edição de imagem, softwares de geometria, etc.

Equação do segundo grau - perímetro, semiperímetro e área de retângulo

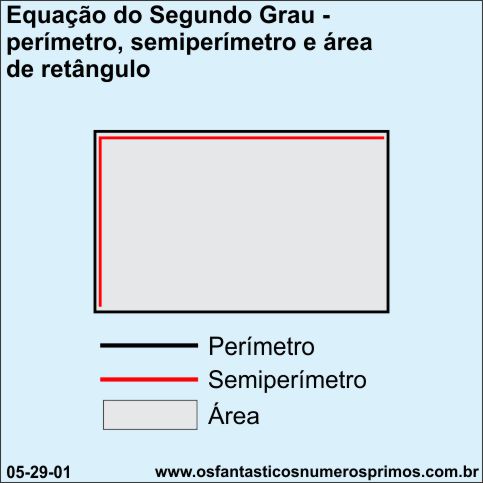
O retângulo possui diversas propriedades geométricas e numéricas e apresenta estreita relação com equação do segundo grau.

A partir de sua forma e dimensões de seus lados são possíveis de se elaborarem equações do segundo grau completas, isto é, equações na forma ax² + bx + c = 0.

Perímetro de um retângulo

Para se saber o perímetro de um polígono, somamos as medidas dos comprimentos de seus lados, no caso do retângulo que possui dois pares de lados congruentes, isto é, dois pares de lados de mesmas medidas de comprimentos, procedemos a seguinte forma:

a) lador de maior comprimento = 2 unidades

b) lado de menor comprimento = 1 unidade

c) (2 x 2) + (2 x 1) = 4 + 2 = 6

d) portanto, o perímetro é de 6 unidades.

A partir deste exemplo, podemos formular outros problemas relacionados a retângulos:

1) O perímetro é 6, e o lado menor do retângulo é 1, qual é a medida da base, isto é, a medida do seu lado maior?

a) a soma dos lados menores subtraído do perímetro do retângulo:

6 - 2 = 4

b) diferença dividida por 2

4 : 2 = 2

cada lado maior do retângulo mede 2 unidades.

2) Quantos retângulos podem ser desenhados com um perímetro de 16 unidades?

Resposta: podem ser desenhados 3 retângulos cujos as medidas dos lados são:

1 + 1 + 7 + 7 = 16

3 + 3 + 5 + 5 = 16

4 + 4 + 4 + 4 = 16

Observação: o quadrado é um caso particular de retângulo.

Área de região retângular

Uma região retangular tem 45cm² e 28 cm de perímetro. Qual é o comprimento da base e da altura?

Podemos pensar da seguinte forma, quais são os dois números cujo produto é 45 e a soma é 14?

Dividindo o perímetro por 2, obtemos o semiperímetro

28 : 2 = 14

14 é a soma da base e altura.

Com quantas somas obtem-se o número 14?

1) 1 + 13 = 14

2) 2 + 14 = 14

3) 3 + 11 = 14

4) 4 + 10 = 14

5) 5 + 9 = 14

6) 8 + 6 = 14

7) 7 + 7 = 14

Com quantas multiplicações obtem-se o número 45?

1) 1 x 45 = 45

2) 3 x 15 = 45

3) 5 x 9 = 45

Portanto, os número 5 e 9 são os dois números que somados resultam 14 e multiplicados resultam 45.

Equação do segundo grau e retângulo

O exemplo anterior também pode ser formulados por meio de equações do segundo grau.

Uma região retangular tem 28cm de perímetro e 45cm² de área. Quais as dimensões dessa região retangular.

Observação: semiperímetro é o perímetro dividido por 2:

28cm : 2 = 14cm

Equação do segundo grau - Fórmula de Bháskara

x² + 14x = 45

Equação do segundo grau na forma:

ax² + bx + c = 0

x² + 14x + 45 = 0

Coeficientes:

a =1

b = 14

c = 45

		- b ± √b² - 4 . a .c
x	=	_____________
		2.a

Delta (Discriminante da equação)

Δ = b² - 4 . a . c

Δ = 14² - 4 . 1 . 45

ii)

Δ = 196 - 180

iii)

O Delta é positivo e maior que 0 (zero), portanto há duas soluções para a equação.

Δ = 16

iv)

		-(+14) ± √16
x	=	_____________
		2

Raízes da equação

		-14 + 4
x'	=	_____	=	- 5
		2

		-14 - 4
x"	=	_____	=	- 9
		2

Equação do Segundo Grau - Método de Completar Quadrados

x² + 14x = 45

Equação do segundo grau na forma:

ax² + bx + c = 0

x² + 14x - 45 = 0

desloca-se o termo independente "c" 45 para o segundo membro.

x² + 14x = - 45

ii)

dividi-se o coeficiente 14 do termo "bx" por 2 e eleve-o ao quadrado, 7² = 49, somando-o ao primeiro e segundo membros.


x²	+	14 x	+	7²	=	-	45	+	7²


x²	+	14 x	+	49	=	-	45	+	49

iii)

fatora-se o primeiro membro...

x² - 14x + 49 = - 45 + 49

iv)

... obtendo um quadrado da soma (Produto Notável)

(x + 7)² = - 45 + 49

extrai-se a raiz quadrada

(x + 7)² = 4

x + 7 = ± √4

x + 7 = ± 2

vi)


x'	=	+ 7 + 2	=	9

vii)


x'	=	+ 7 - 2	=	5

Autor: Ricardo Silva - setembro /2020

Fontes Bibliográficas:

ANDRADE, Bernardino Carneiro de . A evolução histórica da resolução das equações do 2o grau. Departamento de Matemática Pura da Faculdade de Ciências da Universidade do Porto,2000

DANTE, Luiz Roberto . Tudo é Matemática / Luiz Roberto Dante - - 3. ed. - - São Paulo: Àtica, 2009

IEZZI, Gelson. Matêmática e realidade: 9⁰ ano / Gelson Iezzi, Osvaldo Dolce, Antonio Machado. - 6. ed. - São Paulo: Atual, 2009

VALE, Alberton Fagno Albino do. As diferentes Estratégias de Resolução da Equação do Segundo Grau. Dissertação apresentada à Universidade Federal Rural do Semiárido – Ufersa, Mossoró, 2013