


Quadrados Mágicos são conjuntos de números organizados em linhas e colunas de forma que a soma de cada linha, cada coluna bem como cada diagonal tenham sempre a mesma soma, a qual é denominada de Constante Mágica.
Os Quadrados Mágicos podem ser construídos com quadrados quadriculados cujas quantidades de células se referem a números quadrados perfeitos: 9, 16, 25, 36, 49 e assim sucessivamente.
Quadrados Mágicos não estão restrito à forma quadrada, há diversos outros dispositivos numéricos como círculos, triângulos, estrelas, pentagramas, etc. que se assemelham a Quadrados Mágicos.
Quadrados Mágicos podem ser construídos com progressões aritméticas (P.A.s), progressões geométricas (P.G.s) e sequências que não sejam nem PA ou PG como também com símbolos, figuras geométricas, desenhos, etc.
O presente estudo demonstra exemplos de construções de Quadrados Mágicos com sequências numéricas formadas por frações equivalentes.
A partir da fração 1/2 e multiplicando-a pela sequência de números naturais de 1 a 9 obtem-se frações cujos numeradores e denominadores tem como razão 1/2.
Os numeradores aumentam de 1 em 1 unidade.
Os denominadores aumentam de 2 em 2 unidades.
| Sequência de frações equivalentes a 1/2 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||||
| __ | , | __ | , | __ | , | __ | , | __ | , | __ | , | __ | , | __ | , | __ |
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | ||||||||
A progressão artimética têm como numeradores a sequência dos números naturais de 1 a 9 e os denominadores a sequência dos múltiplos de 2.
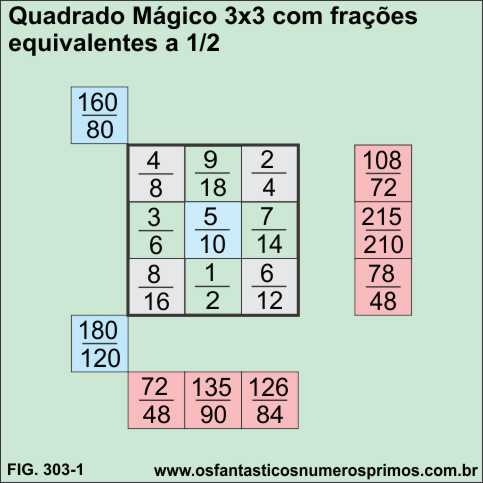
O Quadrado Mágico 3x3 construído com a progressão artimética cuja a razão é 1/2 forma a Constante Mágica de razão 1/2.
As somas de cada linha, cada coluna e diagonais têm como resultados frações cujos numeradores e denominadores apresentam múltiplos de 3.
| Quadrado Mágico 3x3 | ||||
| Frações equivalentes a 1/2 | ||||
| 160 / 80 | ||||
| 4 / 8 | 9 / 18 | 2 / 4 | 108 / 72 | |
| 3 / 6 | 5 / 10 | 7 / 14 | 315 / 210 | |
| 8 / 16 | 1 / 2 | 6 / 12 | 78 / 48 | |
| 72 / 48 | 135 / 90 | 126 / 84 | 180 / 120 | |
Mínimo Múltiplo Comum (8, 18, 4) = 72
| Linha 1 | ||||||||
| 4 | 9 | 2 | 36 + 36 + 36 | 108 | ||||
| __ | + | __ | + | __ | = | __________ | = | __ |
| 8 | 18 | 4 | 72 | 72 | ||||
Mínimo Múltiplo Comum (6, 10, 14) = 210
| Linha 2 | ||||||||
| 3 | 5 | 7 | 105 + 105 + 105 | 315 | ||||
| __ | + | __ | + | __ | = | __________ | = | __ |
| 6 | 10 | 14 | 210 | 210 | ||||
Mínimo Múltiplo Comum (16, 2, 12) = 48
| Linha 3 | ||||||||
| 8 | 1 | 6 | 24 + 24 + 24 | 74 | ||||
| __ | + | __ | + | __ | = | __________ | = | __ |
| 16 | 2 | 12 | 48 | 48 | ||||
Mínimo Múltiplo Comum (8, 6, 16) = 48
| coluna 1 | ||||||||
| 4 | 3 | 8 | 24 + 24 + 24 | 72 | ||||
| __ | + | __ | + | __ | = | __________ | = | __ |
| 8 | 6 | 16 | 48 | 48 | ||||
Mínimo Múltiplo Comum (18, 10, 2) = 90
| coluna 2 | ||||||||
| 9 | 5 | 1 | 45 + 45 + 45 | 135 | ||||
| __ | + | __ | + | __ | = | __________ | = | __ |
| 18 | 10 | 2 | 90 | 90 | ||||
Mínimo Múltiplo Comum (4, 14, 12) = 84
| coluna 3 | ||||||||
| 2 | 7 | 6 | 42 + 42 + 42 | 126 | ||||
| __ | + | __ | + | __ | = | __________ | = | __ |
| 4 | 14 | 12 | 84 | 84 | ||||
Mínimo Múltiplo Comum (8, 10, 12) = 120
| diagonal principal | ||||||||
| 4 | 5 | 6 | 60 + 60 + 60 | 180 | ||||
| __ | + | __ | + | __ | = | __________ | = | __ |
| 8 | 10 | 12 | 120 | 120 | ||||
Mínimo Múltiplo Comum (16, 10, 4) = 80
| diagonal secundária | ||||||||
| 8 | 5 | 2 | 40 + 40 + 40 | 120 | ||||
| __ | + | __ | + | __ | = | __________ | = | __ |
| 16 | 10 | 4 | 80 | 80 | ||||
A partir da fração 2/3 e multiplicando-a pela sequência de números naturais de 1 a 9 obtem-se frações cujos numeradores e denominadores tem como razão 2/3.
Os numeradores aumentam de 2 em 2 unidades.
Os denominadores aumentam de 3 em 3 unidades.
| Sequência de frações equivalentes a 2/3 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | ||||||||
| __ | , | __ | , | __ | , | __ | , | __ | , | __ | , | __ | , | __ | , | __ |
| 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | ||||||||
A progressão artimética têm como numeradores a sequência dos números pares e os denominadores a sequência dos múltiplos de 3.
O Quadrado Mágico 3x3 construído com a progressão artimética cuja a razão é 2/3 forma Constante Mágica de razão 2.
As somas de cada linha, cada coluna e diagonais têm como resultados frações cujos numeradores e denominadores apresentam múltiplos de 3.
| Quadrado Mágico 3x3 | ||||
| Frações equivalentes a 2/3 | ||||
| 240 / 120 | ||||
| 8 / 12 | 18 / 27 | 4 / 6 | 216 / 108 | |
| 6 / 9 | 10 / 15 | 14 / 21 | 630 / 315 | |
| 16 / 24 | 2 / 3 | 12 / 18 | 144 / 72 | |
| 144 / 72 | 270 / 135 | 252 / 126 | 360 / 180 | |
A partir da fração 3/4 e multiplicando-a pela sequência de números naturais de 1 a 9 obtem-se frações cujos numeradores e denominadores tem como razão 3/4.
Os numeradores aumentam de 3 em 3 unidades.
Os denominadores aumentam de 4 em 4 unidades.
| Progressão Aritmética de razão 3/4 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | ||||||||
| __ | , | __ | , | __ | , | __ | , | __ | , | __ | , | __ | , | __ | , | __ |
| 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | ||||||||
A progressão artimética têm como numeradores a sequência dos números múltiplos de 3 e os denominadores a sequência dos múltiplos de 4.
O Quadrado Mágico 3x3 construído com a progressão artimética cuja a razão é 3/4 forma Constante Mágica de razão 2,25.
As somas de cada linha, cada coluna e diagonais têm como resultados frações cujos numeradores e denominadores apresentam múltiplos de 3.
| Quadrado Mágico 3x3 | ||||
| Frações equivalentes a 3/4 | ||||
| 360 / 160 | ||||
| 12 / 16 | 27 / 36 | 6 / 8 | 324 / 144 | |
| 9 / 12 | 15 / 20 | 21 / 28 | 945 / 420 | |
| 24 / 32 | 3 / 4 | 18 / 24 | 216 / 96 | |
| 216 / 96 | 405 / 180 | 378 / 168 | 540 / 240 | |
Autor: Ricardo Silva - novembro/2020
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato