


Números figurados são números que podem ser representados por arranjos de pontos com os quais podem ser formados figuras geométrias como triângulos, quadrados, pentágonos, hexágonos, etc.
A partir de números triagulares podem ser construídos os demais números figurados que representam figuras geométricas regulares.
Veja matérias relacionadas:
011-estudos-248-numeros-figurados-e-numeros-poligonais.
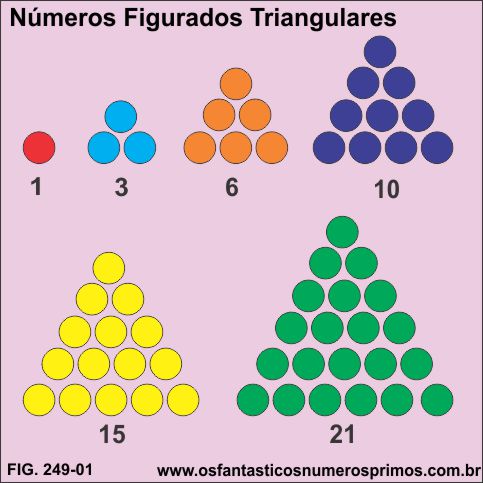
Obtem-se números triangulares através da soma de números consecutivos:
1
1 + 2 = 3
1 + 2 + 3 = 6
1 + 2 + 3 + 4 = 10
1 + 2 + 3 + 4 + 5 = 15
1 + 2 + 3 + 4 + 5 + 6 = 21
da mesma forma, a partir de um ponto acrescenta-se outras quantidades em um dos lados para se formar triângulos equiláteros.
Partindo-se de um ponto central, os demais hexágonos são formados marcando-se os vértices e posteriormente distribuindo os pontos em seus lados de forma que os hexágonos fiquem equidistantes.
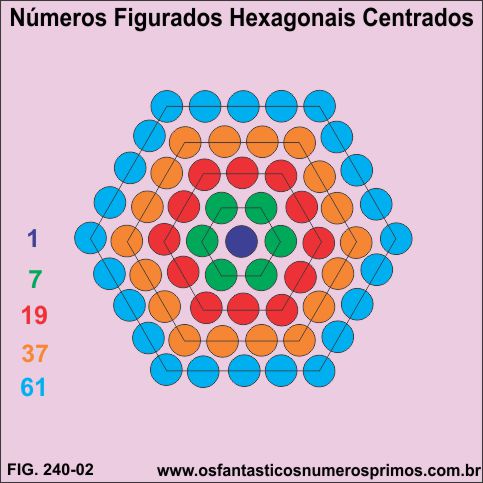
Determinados números figurados triangulares apresentam números figurados hexagonais centrados inscritos.
Os números 10, 28, 55, 91, 136 e outros estão em rol de números figurados triangulares em que contém figuras de hexágonos centrados inscritos.
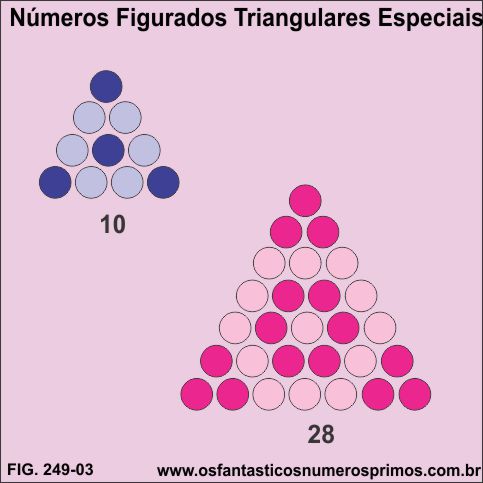
Sobrepondo dois triângulos figurados de 10 pontos forma-se um hexágono estrelado de 13 pontos.
Cada lado do hexágono contêm um triângulo figurado de 1 ponto, totalizando 6 triângulo figurados.
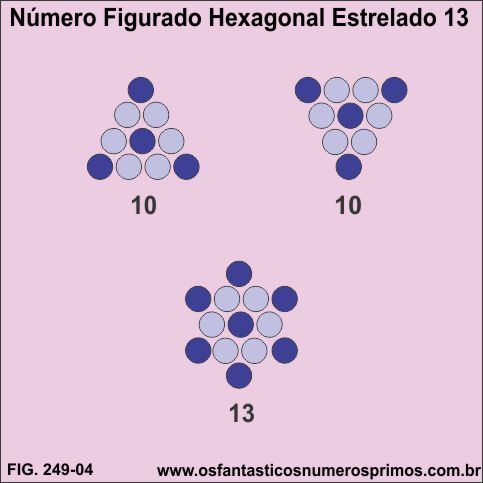
Hexágono estrelado construído com 13 pontos e numerados com os 13 primeiros números naturais apresenta as seguintes relações numéricas com hexágono centrado de 7 pontos:
a) o número 7, que corresponde ao segundo hexágono centrado se encontra no centro do hexágono estrelado;
b) a soma de dois termos equidistante do centro do hexágono estrelado tem como resultado 14, que é o dobro de 7;
c) a soma dos números: 1 + 5 + 12 + 13 + 9 + 2 = 42 que o produto de 6x7;
d) a soma dos números: 3 + 4 + 8 + 11 + 10 + 6 = 42 que o produto de 6x7;
e) a soma de três números em sentido diagonal tem como resultado 21.

Sobrepondo dois triângulos figurados de 28 pontos forma-se um hexágono estrelar de 37 pontos.
Cada lado do hexágono contêm um triângulo figurado de 3 pontos, totalizando 6 triângulo figurados.

Hexágono estrelado construído com 37 pontos e numerados com os 37 primeiros números naturais apresenta as seguintes relações numéricas com hexágono centrado de 19 pontos:
a) o número 19, que corresponde ao terceiro hexágono centrado se encontra no centro do hexágono estrelado;
b) a soma de dois termos equidistante do centro do hexágono estrelado tem como resultado 38, que é o dobro de 19;
c) a soma dos números: 1 + 10 + 34 + 37 + 28 + 4 = 114 que o produto de 6x19;
d) a soma dos números: 2 + 3 + 9 + 16 + 27 + 33 + 36 + 35 + 29 + 28 + 11 + 5 = 228 que o produto de 12x19;
e) a soma dos números: 6 + 7 + 8 + 15 + 21 + 26 + 32 + 31 + 30 + 23 + 17 + 12 = 228 que o produto de 12x19;
f) a soma dos números: 13 + 14 + 20 + 25 + 24 + 18 = 114 que o produto de 6x19.

Justapondo-se triângulos equiláteros é possível construir hexágonos estrelados.
Os triângulos equiláteros estão numerados, assim como seus vértices e em quantidades de múltiplos de 6 e apresentam interessantes propriedades geométricas e numéricas com hexágonos estrelados centrados construídos por pontos.
Hexágono estrelar construído com 12 triângulos equiláteros.
Dispondo os termos da sequência (1, 2,...11, 12) em uma tabela verifica-se a propriedade de uma progressão aritmética finita em que a soma de dois termos equidistantes dos extremos é igual à soma dos extremos.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | = | 78 |
| 1 | 12 | = | 13 | ||||||||||
| 2 | 11 | = | 13 | ||||||||||
| 3 | 10 | = | 13 | ||||||||||
| 4 | 9 | = | 13 | ||||||||||
| 5 | 8 | = | 13 | ||||||||||
| 6 | 7 | = | 13 |
A mesma propriedade se observa na disposição da sequência numérica (1, 2, 3,...10, 11, 12) no formato de estrela de 6 pontas.
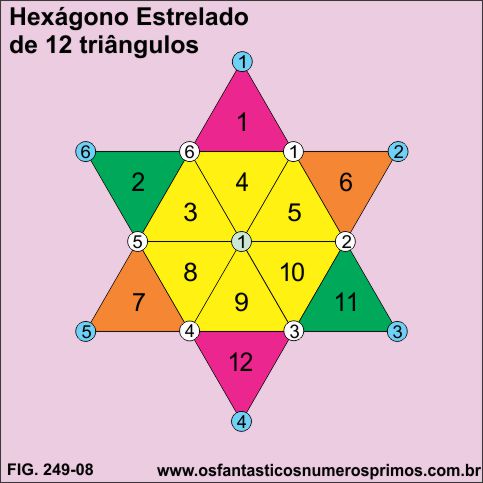
A soma dos termos 1 + 2 + .....+ 11 + 12 = 78
O 120 número triangular é 78.
1 + 6 + 11 + 12 + 7 + 2 = 39
39 é a metade de 78.
A quantidade de triângulos equiláteros que formam as pontas da estrela é igual a quantidade que formam o hexágono.
6 triângulos equiláteros formam as pontas da estrela.
6 triângulos equiláteros formam o hexágono.
4 + 5 + 10 + 9 + 8 + 3 = 39
39 é a metade de 78.
A quantidade de triângulos equiláteros que formam o hexágono é igual a quantidade que formam as pontas da estrela.
6 triângulos equiláteros formam o hexágono.
6 triângulos equiláteros formam as pontas da estrela.
A quantidade de vértices é igual a soma de dois termos equidistantes.
13 vértices.
13 é o hexágono estrelar centrado construído por pontos.
Hexágono estrelado construído com 48 triângulos equiláteros.
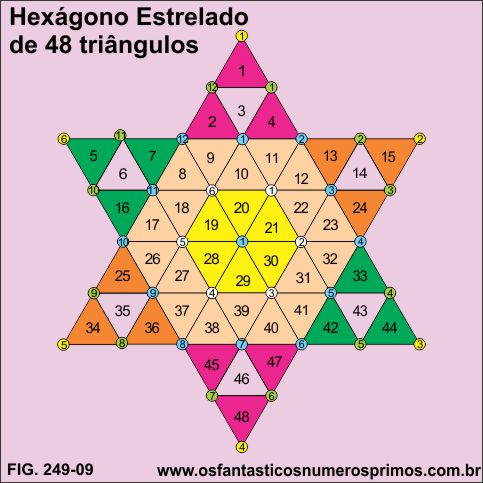
A soma dos termos 1 + 2 + .....+ 47 + 48 = 1176
O 480 número triangular é 1176.
| Sub-total | ||||
| 0 | ||||
| 1 | 2 | 3 | 4 | 10 |
| 13 | 14 | 15 | 24 | 66 |
| 33 | 42 | 43 | 44 | 162 |
| 45 | 46 | 47 | 48 | 186 |
| 25 | 34 | 35 | 36 | 130 |
| 5 | 6 | 7 | 16 | 34 |
| 0 | ||||
| Total | 588 |
588 é a metade de 1176.
A quantidade de triângulos equiláteros que formam as pontas da estrela é igual a quantidade que formam os hexágonos.
24 triângulos equiláteros formam as pontas da estrela.
24 triângulos equiláteros formam os dois hexágonos.
| Sub-total | ||||||
| 0 | ||||||
| 19 | 20 | 21 | 28 | 29 | 30 | 147 |
| 0 | ||||||
| 8 | 9 | 10 | 11 | 12 | 50 | |
| 17 | 18 | 22 | 23 | 80 | ||
| 26 | 27 | 31 | 32 | 116 | ||
| 37 | 38 | 39 | 40 | 41 | 195 | |
| 0 | ||||||
| Total | 588 |
588 é a metade de 1176.
A quantidade de triângulos equiláteros que formam os hexágonos é igual a quantidade que formam as pontas da estrela.
24 triângulos equiláteros formam os hexágonos.
24 triângulos equiláteros formam as pontas da estrela.
37 vértices.
37 é o hexágono estrelar centrado construído por pontos.
Tabela com os 50 primeiro números hexagonais estrelados.
Pode-se obter números hexagonais estrelados por meio da seguinte fórmula algébrica:
| 12 { n (n + 1) } + 1 |
| _______ |
| 2 |
ou de modo prático multiplicando o número 12 por um número triangular somado de 1 unidade.
O número 1 por convenção é um número poligonal.
1
(12 x 1) + 1 = 13
(12 x 3) + 1 = 37
(12 x 6) + 1 = 73
(12 x 10) + 1 = 121
(12 x 15) + 1 = 181
| Números | |
|---|---|
| Hexagonais Estrelados | |
| posição | números |
| /ordem | hexagonais estrelados |
| 1 | 1 |
| 2 | 13 |
| 3 | 37 |
| 4 | 73 |
| 5 | 121 |
| 6 | 181 |
| 7 | 253 |
| 8 | 337 |
| 9 | 433 |
| 10 | 541 |
| 11 | 661 |
| 12 | 793 |
| 13 | 937 |
| 14 | 1093 |
| 15 | 1261 |
| 16 | 1441 |
| 17 | 1633 |
| 18 | 1837 |
| 19 | 2053 |
| 20 | 2281 |
| 21 | 2521 |
| 22 | 2773 |
| 23 | 3037 |
| 24 | 3313 |
| 25 | 3601 |
| 26 | 3901 |
| 27 | 4213 |
| 28 | 4537 |
| 29 | 4873 |
| 30 | 5221 |
| 31 | 5581 |
| 32 | 5953 |
| 33 | 6337 |
| 34 | 6733 |
| 35 | 7141 |
| 36 | 7561 |
| 37 | 7993 |
| 38 | 8437 |
| 39 | 8893 |
| 40 | 9361 |
| 41 | 9841 |
| 42 | 10333 |
| 43 | 10837 |
| 44 | 11353 |
| 45 | 11881 |
| 46 | 12421 |
| 47 | 12973 |
| 48 | 13537 |
| 49 | 14113 |
| 50 | 14701 |
| wwww.osfantasticosnúmerosprimos.com.br | |
Autor: Ricardo Silva - janeiro/2020
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato