Página de estudos de matemática e sequências numéricas

Múltiplos de 3 e Números de Mersenne - 503

Potências de base 2 é uma progressão geométrica cujo primeiro termo é 1 unidade e a sua razão é 2.

Podemos obter potências de base 2, multiplicando o número 2 por ele memo sequencialmente, ou elevando o número 2 a expoentes com números naturais.

Potências de base 2 menos 1 unidade têm como resultados Números de Mersenne / Números Quase-Potência de base 2.

Base 2 elevada a expoente pares geram potências que são números quadrados perfeitos.

Potência de Base 2 que são números quadrados perfeitos menos 1 unidade, são números divisíveis por 3.

O presente estudo demonstra que determinados Números de Mersenne / Números Quase-Potência de Base 2 divididos por 3 geram quocientes que divididos novamente por 3 geram quocientes que são produtos de 2 números primos distintos, e entre eles, os próprios Números Primos de Mersenne.

Euclides e os números perfeitos

No IX Livro – proposição 36 dos Elementos de Euclides de Alexandria (300 a.C) contêm a definição de números perfeitos e a seguinte proposição:

"Se tantos números quantos se queira começando a partir da unidade forem dispostos continuamente numa proporção duplicada até que a soma de todos resulte num número primo, e se a soma multiplicada pelo último origina algum número, então o produto será um número perfeito".

Em linguagem matemática temos que se 2ⁿ-1 é um número primo então a fórmula 2ⁿ⁻¹(2ⁿ-1) resulta em um número perfeito.

Os gregos antigos estavam limitados aos quatro primeiros números dados pela fórmula de Euclides 2ⁿ⁻¹ ( 2ⁿ-1 ).[1]

Números Primos de Mersenne

Marin Mersenne (1588-1648) em sua Obra Cogita physico-mathematica (1644), conjecturou em 1644 que os números: Mp = 2^p-1 é primo (p≥1), são primos para 2, 3, 5, 7, 13, 17, 31, 67, 127, 257 e compostos para p>257.

Posteriormente com Computadores e Softwares Matemáticos foi possível verificar que M61 é primo, M67 é composto, M89 é primo, M107 é primo e M257 é composto.[1]

Observação: nem todo Número de Mersenne é um número primo.

Projeto GIMPS

George Woltman, estadunidense formado em Ciências da Computação. Em 1996, criou um Grupo de Estudo (GIMPS - Great Internet Mersenne Prime Search) que procura por números primos de Mersenne e que foi o responsável pela descoberta dos últimos dezesseis maiores números de Mersenne até o momento, o M51 foi encontrado em dezembro de 2018 e tem mais de 24 milhões de dígitos.[1]

Potências de base 2

Potências de base 2 estão estritamente relacionadas a números primos, números perfeitos e a Números de Mersenne.

Potências de base 2 apresentam várias propriedades matemáticas e, entre elas:

Soma consecutiva de potências de base 2

A soma consecutiva de potências de base 2 têm como resultados números ímpares e, entre eles, Números de Mersenne.

Potências de base 2 também são denominadas de Números Quase Potências de Base 2, pois, são 1 unidade menor que a própria potência de base 2.

1

1 + 2 = 3

1 + 2 + 4 = 7

1 + 2 + 4 + 8 = 15

1 + 2 + 4 + 8 + 16 = 31

1 + 2 + 4 + 8 + 16 + 32 = 63

Soma de divisores próprios de potências de base 2

A soma de divisores próprios de potências de base 2 têm como resultados números ímpares, e entre eles, Números de Mersenne.

A soma de divisores póprios de potências de base 2 também é denominada de Números Quase-Potências de Base 2, pois, são 1 unidade menor que a própria potência de base 2.

2¹ = 2

D(2): { 1, 2 }

1

2² = 4

D(4): { 1, 2, 4 }

1 + 2 = 3

2³ = 8

D(8): { 1, 2, 4, 8 }

1 + 2 + 4 = 7

2⁴ = 16

D(16): { 1, 2, 4, 8, 16 }

1 + 2 + 4 + 8 = 15

2⁵ = 32

D(32): { 1, 2, 4, 8, 16, 32 }

1 + 2 + 4 + 8 + 16 = 31

Potências de base 2 e expoentes pares

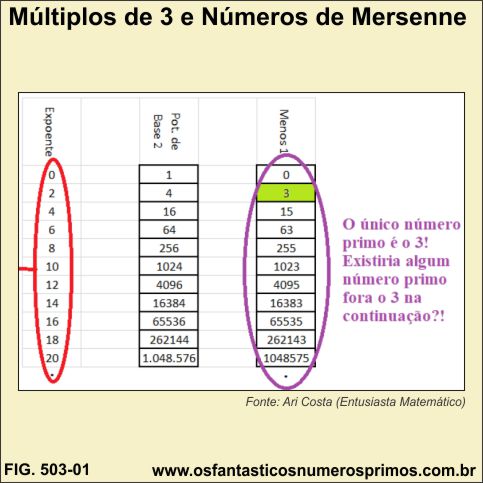
A tabela a seguir apresenta as 26 primeiras potências de base 2 e suas relações com números quase potências de base 2, múltiplos de 3 e Números de Mersenne.

Todo número natural elevado a expoente par tem como resultado um número quadrado perfeito.

A base 2 elevada a expoente par gera um número quadrado perfeito.

Observação: por praticidade, as ordens das linhas seguem as ordens dos expoentes da base 2: 2¹ ; linha 1, 2² ; linha 2 e assim sucessivamente (descartando-se o expoente 0).

Potência de base 2 e expoente par

Toda potência de base 2 elevada a expoente par, subtraída 1 unidade e dividida por 3 têm como quociente um número múltiplo de 3, isto é, um número de Mersenne /número quase potência de base 2.

Exemplos:

a) linha 2

2² = 4

4 - 1 = 3 (número quase potência de base 2)

3 é múltiplo de 3

b) linha 4

2⁴ = 16

16 - 1 = 15 (número quase potência de base 2)

15 é múltiplo de 3

Números quase potência de base 2

Determinados números quase potências de base 2 divididos por 3 apresentam quocientes que são produtos de 2 números primos distintos e, entre eles, Número Primo de Mersenne.

Observação: números que são produtos de 2 números primos distintos, são números que possuem quantidades de divisores em números quadrados perfeitos.

Números (bases) e suas potências que possuem divisores em quantidades de números quadrados perfeitos são números com os quais são possíveis de se contruirem quadrados mágicos multiplicativos sequencialmente.

Para mais informações, veja abaixo, Matérias Relacionadas!

Exemplos:

a) linha 6 (célula azul)

2⁶ = 64

64 - 1 = 63 (número quase potência de base 2)

63 : 3 = 21

O número 21 é produto de 2 números primos distintos

3 x 7 = 21

O segundo fator 7 é um Número Primo de Mersenne.

Observação importantíssima

O número 7 ( Número de Mersenne ) aparece primeiro na linha 3, onde o expoente é 3.

2³ = 8

8 - 1 = 7 (número quase potência de base 2)

As regularidades e conexões entre os números na tabela se constata pelo fato de que o expoente 3 é a metade do expoente 6.

O número 7 (Número de Mersenne), linha 3, "expoente 3" é verificado e comprovado que é realmente Número de Mersenne na linha 6 "expoente 6" e por ser o segundo fator da multiplicação:

3 x 7 = 21

b) linha 5 (célula lilás)

2⁵ = 32

32 - 1 = 31 (número quase potência de base 2)

O número 31 não é divisível por 3.

O número 31 é um número primo.

O número 31 é um número primo de Mersenne.

O número 31 também aparece na linha 10.

2¹⁰ = 1024

1024 - 1 = 1023 (número quase potência de base 2)

1023 : 3 = 341

O número 341 é produto de 2 números primos distintos:

11 x 31 = 341

O segundo fator 31 é um Número Primo de Mersenne.

Observação importantíssima

O número 31 ( Número de Mersenne ) aparece primeiro na linha 5, onde o expoente é 5.

2⁵ = 32

32 - 1 = 31 (número quase potência de base 2)

As regularidades e conexões entre os números na tabela se constata pelo fato de que o expoente 5 é a metade do expoente 10.

O número 31 (Número de Mersenne), linha 5, "expoente 5" é verificado e comprovado que é realmente Número de Mersenne na linha 10 "expoente 10" e por ser o segundo fator da multiplicação:

11 x 31 = 341

Fórmulas para Números Primos de Mersenne

A partir dos exemplos acima demonstrados, deduziu-se as seguintes fórmulas:

Fórmula 1

para n igual ou maior que 3.

Se o quociente entre a base 2 elevada a expoente par menos 1 unidade e o número 3 for produto de 2 números primos distintos, então um dos números primos é um Número Primo de Mersenne.

Exemplo:

i)

ii)

iii)

iv)

v)

vi)

21 = 3 x 7

21 é produto de 2 números primos distintos.

O segundo fator 7 é um Número Primo de Mersenne.

Fórmula 2

Se o quociente entre a base 2 elevada ao dobro de um número primo menos 1 unidade e o número 3 for produto de 2 números primos distintos, então um dos números primos é um Número Primo de Mersenne.

Conclusão

Verifica-se que são possíveis a partir dos próprios Números de Mersenne (Números quase-potências de base 2) que são números compostos e divisíveis por 3 comprovar os próprios Números Primos de Mersenne.

Os cálculos para se montar a tabela com Números de Mersenne, foram realizados até a potência:

2¹⁰⁶ = 81 129 638 414 606 681 695 789 005 144 064 (número com 32 algarismos) na Calculadora Científica do Sistema Operacional Windows 8.1, em um PC com Processador Dual Core 2,5 GHz e RAM 4 GB.

Os cálculos para se obterem os divisores dos números foram realizados em:

014-013-calculadora-divisores-numero-natural-on-line

aqui do WebSite Os Fantásticos Números Primos, totalizando os 7 primeiros Números Primos de Mersenne, quantidade esta limitada até o presente momento pela capacidade de computação e infra-estrutura.

Nos WebSites:

https://pt.planetcalc.com/

https://www.omnicalculator.com/

https://pt.numberempire.com/

https://numbermatics.com/

foram realizadas as verificações dos resultados da tabela.

O WebSite Os Fantásticos Números Primos faz um convite a entusiastas matemáticos, estudantes, professores, profissionais da área de exatas, empresas de tecnologia, centros de pesquisas, universidades, etc. que possa disponibilizar recursos humanos / recursos materiais para desenvolvimento de projeto computacional para se encontrar Números Primos de Mersenne a partir dos estudos aqui descritos.

Autores: Ricardo Silva e Ari Costa - julho/2024

Fontes Bibliográficas:

SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023

SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012

[1] SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020

SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022

SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021

SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017

SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Matérias relacionadas:

011-estudos-151-produto-numero-impar-com-sua-ordem

011-estudos-203-quadrados-magicos-multiplicativos-e-divisores-de-36

011-estudos-263-numeros-perfeitos-numeros-quase-quadrados-perfeitos

011-estudos-264-numeros-perfeitos-potencias-base12

011-estudos-265-numeros-primos-e-os-matematicamentes-brilhantes

011-estudos-266-numeros-primos-e-as-mentes-matematicas

011-estudos-306-potencias-base-2-soma-progressoes-geometricas

011-estudos-503-multiplos-tres-e-numeros-de-mesenne

011-estudos-513-numeros-perfeitos-raizes-numeros-quadrados-perfeitos

011-estudos-514-potencias-base-2-produtos-numeros-consecutivos

011-estudos-515-numeros-mersenne-e-raizes-e-quadrados

011-estudos-516-numeros-mersenne-um-novo-metodo

011-estudos-517-tabela-numeros-mersenne

Livro digital (e-book)

Escada de Theon

e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)

Números Primos e o

Método Números Atraentes

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)

Progressões Aritméticas e Geométricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Tabuada de Pythagoras

e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Estudos de Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Os Fantásticos Números Primos

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)

Ternos Pitagóricos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Senhores Professores de Matemática,

Profissionais de Exatas e

Entusiastas Matemáticos

Recebam GRATUITAMENTE

o E-book

Triângulo Retângulo

 

FAÇA A SUA SOLICITAÇÃO

AGORA MESMO ATRAVÉS

DO E-MAIL:

contato@osfantasticos numerosprimos.com.br

Livro Digital (e-book) Descobrindo Números Primos a partir de Números Compostos

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (E-book) Quadrados Mágicos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)
Números Triangulares e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Manual digital (E-book) Quadrado Mágico Triplo

LIVRO GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)

Números Perfeitos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Manual Digital (E-book) Multiplicação através da soma de múltiplos

LIVRO GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Prezado visitante, o conteúdo do

WebSite Os Fantásticos Números Primos

está protegido por direitos autorais.

O uso acadêmico e escolar está liberado,

desde que informando ao autor o local e

o meio em que será utilizado e divulgado,

através do e-mail:

contato@osfantasticosnumerosprimos.com.br

O uso comercial é proibido.