


Várias são as estórias que se contam sobre Johann Carl Friedrich Gauss (1777-1855) quando criança cujo professor solicitou a ele e aos colegas de classe que somassem a sequência dos números de 1 a 100.
O Sr. Brian Hayes (com muita ajuda de seus amigos) tem publicado no seguinte link:
http://bit-player.org/wp-content
uma coletânea com mais de 140 estórias do pequeno grande Gauss e entre elas a que está publicada no livro A Música do Números Primos do Professor Marcus Du Satoy, pag. 33 - edição brasileira:
"...Em vez de enfrentar o problema de frente, Gauss pensou lateralmente. Ele argumentou que a melhor maneira de descobrir quantos grãos havia em um triângulo com 100 linhas era pegar um segundo triângulo semelhante de grãos que poderia ser colocado de cabeça para baixo no topo do primeiro triângulo. Agora Gauss tinha um retângulo com 101 linhas, cada uma contendo 100 grãos. Calcular o número total de grãos neste retângulo construído com os dois triângulos foi fácil: há um total de 101 × 100 = 10,100 grãos. Portanto, um triângulo deve conter metade desse número, a saber, 1/2 × 101 × 100 = 5.050. Não há nada de especial aqui sobre 100. Substitua por N e você terá a fórmula 1/2 × (N + 1) × N."
O presente estudo demonstra novas propriedades matemáticas relacionadas a números triangulares e as somas de sequências de múltiplos consecutivos de números naturais:
1) números triangulares são divisores de somas de sequências de múltiplos consecutivos de números naturais;
2) o produto de um número natural por um número triângular têm como resultado a soma de sequências de múltiplos consecutivos desse número natural.
3) As somas de sequências de múltiplos consecutivos de números naturais são múltiplos de números triangulares.
A soma de números naturais consecutivos têm como resultados números triangulares.
Números triangulares, também denominados de números figurados, números poligonais, números geométricos, são números que podem representar figuras geométricas por meio de arranjos de pontos.
1
1 + 2 = 3
1 + 2 + 3 = 6
1 + 2 + 3 + 4 = 10
1 + 2 + 3 + 4 + 5 = 15
1 + 2 + 3 + 4 + 5 + 6 = 21
1 + 2 + 3 + 4 + 5 + 6 + 7 = 28
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 = 66
O livro digital Números Triangulares e Sequências Numéricas aborda através de vários exemplos com ilustrações e tabelas estudos de como gerar números triangulares e a sua relação com números quadrados perfeitos, números cúbicos e vice-versa, utilizando como base figuras geométricas de triângulos, quadrados, hexágonos, etc.
Por meio da fórmula a seguir, pode-se determinar a soma de n termos de uma Progressão Aritmética (PA).
Substituindo determinados números da sequência (1, 2, 3, ..., 98, 99, 100) nos seguintes termos abaixo e aplicando-os na fórmula, podemos obter a soma dos 100 primeiro números naturais:
a1 - primeiro termo = 1
an - último termo = 100
n - quantidade de termos = 100
Sn - soma do termos = ?
| (a1 + an) | ||||
| Sn | = | _____________ | x | n |
| 2 |
| (1 + 100) | ||||
| S100 | = | _________ | x | 100 |
| 2 |
| 101 | ||||
| S100 | = | ____ | x | 100 |
| 2 |
| 10100 | ||||
| S100 | = | ______ | ||
| 2 |
| S100 | = | 5050 |
A soma de todos os termos de 1 a 100 = 5050.
Multiplicando o número 2 pela sequência de números naturais, obtêm-se múltiplos de 2 e consequentemente sequência de números pares.
Os múltiplos de 2 formam uma Progressão Aritmética cujo primeiro termo é 2 e razão 2.
| Tabuada do 2 | ||||
|---|---|---|---|---|
| naturais | Múltiplos | |||
| de 2 | ||||
| 1 | x | 2 | = | 2 |
| 2 | x | 2 | = | 4 |
| 3 | x | 2 | = | 6 |
| 4 | x | 2 | = | 8 |
| 5 | x | 2 | = | 10 |
| 6 | x | 2 | = | 12 |
| 7 | x | 2 | = | 14 |
| 8 | x | 2 | = | 16 |
| 9 | x | 2 | = | 18 |
| 10 | x | 2 | = | 20 |
| www.osfantasticosnumerosprimos.com.br | ||||
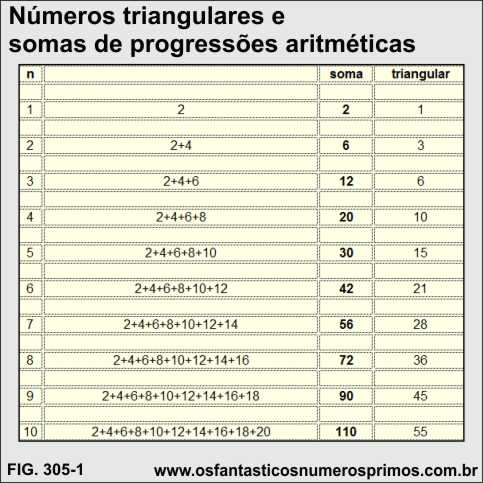
A soma de múltiplos de 2 consecutivos têm como resultado o dobro de um número triangular.
| Soma de múltiplos de 2 consecutivos | |||
|---|---|---|---|
| n | soma | triangular | |
| 1 | 2 | 2 | 1 |
| 2 | 2 + 4 | 6 | 3 |
| 3 | 2 + 4 + 6 | 12 | 6 |
| 4 | 2 + 4 + 6 + 8 | 20 | 10 |
| 5 | 2 + 4 + 6 + 8 + 10 | 30 | 15 |
| 6 | 2 + 4 + 6 + 8 + 10 + 12 | 42 | 21 |
| 7 | 2 + 4 + 6 + 8 + 10 + 12 + 14 | 56 | 28 |
| 8 | 2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 | 72 | 36 |
| 9 | 2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 + 18 | 90 | 45 |
| 10 | 2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 + 20 | 110 | 55 |
| www.osfantasticosnumerosprimos.com.br | |||
O produto de 2 pelo triangular 3 é igual a 6.
6 é a soma dos múltiplos 2 e 4.
6 é o dobro do triangular 3.
3 é o segundo número triangular.
As parcelas 2 e 4 se encontram na segunda linha da tabela.
O produto de 2 pelo triangular 6 é igual a 12.
12 é a soma dos múltiplos 2, 4 e 6.
12 é dobro do triangular 6.
6 é o terceiro número triangular.
As parcelas 2, 4 e 6 se encontram na terceira linha da tabela.
O produto de 2 pelo triangular 10 é igual a 20.
20 é a soma dos múltiplos 2, 4, 6 e 8.
20 é dobro do triangular 10.
10 é o quarto número triangular.
As parcelas 2, 4, 6 e 8 se encontram na quarta linha da tabela.
Multiplicando o número 3 pela sequência de números naturais, obtêm-se sequência de múltiplos de 3.
Os múltiplos de 3 formam uma Progressão Aritmética cujo primeiro termo é 3 e razão 3.
| Tabuada do 3 | ||||
|---|---|---|---|---|
| naturais | Múltiplos | |||
| de 3 | ||||
| 1 | x | 3 | = | 3 |
| 2 | x | 3 | = | 6 |
| 3 | x | 3 | = | 9 |
| 4 | x | 3 | = | 12 |
| 5 | x | 3 | = | 15 |
| 6 | x | 3 | = | 18 |
| 7 | x | 3 | = | 21 |
| 8 | x | 3 | = | 24 |
| 9 | x | 3 | = | 27 |
| 10 | x | 3 | = | 30 |
| www.osfantasticosnumerosprimos.com.br | ||||
A soma de múltiplos de 3 consecutivos têm como resultado o triplo de um número triangular.
| Soma de múltiplos de 3 consecutivos | |||
|---|---|---|---|
| n | soma | triangular | |
| 1 | 3 | 3 | 1 |
| 2 | 3 + 6 | 9 | 3 |
| 3 | 3 + 6 + 9 | 18 | 6 |
| 4 | 3 + 6 + 9 + 12 | 30 | 10 |
| 5 | 3 + 6 + 9 + 12 + 15 | 45 | 15 |
| 6 | 3 + 6 + 9 + 12 + 15 + 18 | 63 | 21 |
| 7 | 3 + 6 + 9 + 12 + 15 + 18 + 21 | 84 | 28 |
| 8 | 3 + 6 + 9 + 12 + 15 + 18 + 21 + 24 | 108 | 36 |
| 9 | 3 + 6 + 9 + 12 + 15 + 18 + 21 + 24 + 27 | 135 | 45 |
| 10 | 3 + 6 + 9 + 12 + ... + 24 + 27 + 30 | 165 | 55 |
| www.osfantasticosnumerosprimos.com.br | |||
O produto de 3 pelo triangular 3 é igual a 9.
9 é a soma dos múltiplos 3 e 6.
9 é o triplo do triangular 3.
3 é o segundo número triangular.
As parcelas 3 e 6 se encontram na segunda linha da tabela.
O produto de 3 pelo triangular 6 é igual a 18.
18 é a soma dos múltiplos 3, 6 e 9.
18 é o triplo do triangular 6.
6 é o terceiro número triangular.
As parcelas 3, 6 e 9 se encontram na terceira linha da tabela.
O produto de 3 pelo triangular 10 é igual a 30.
30 é a soma dos múltiplos 3, 6, 9 e 12.
30 é o triplo do triangular 10.
10 é o quarto número triangular.
As parcelas 3, 6, 9 e 12 se encontram na quarta linha da tabela.
Multiplicando o número 4 pela sequência de números naturais, obtêm-se sequência de múltiplos de 4.
Os múltiplos de 4 formam uma Progressão Aritmética cujo primeiro termo é 4 e razão 4.
| Tabuada do 4 | ||||
|---|---|---|---|---|
| naturais | Múltiplos | |||
| de 4 | ||||
| 1 | x | 4 | = | 4 |
| 2 | x | 4 | = | 8 |
| 3 | x | 4 | = | 12 |
| 4 | x | 4 | = | 16 |
| 5 | x | 4 | = | 20 |
| 6 | x | 4 | = | 24 |
| 7 | x | 4 | = | 28 |
| 8 | x | 4 | = | 32 |
| 9 | x | 4 | = | 36 |
| 10 | x | 4 | = | 40 |
| www.osfantasticosnumerosprimos.com.br | ||||
A soma de múltiplos de 4 consecutivos têm como resultado o quádruplo de um número triangular.
| Soma de múltiplos de 4 consecutivos | |||
|---|---|---|---|
| n | soma | triangular | |
| 1 | 4 | 4 | 1 |
| 2 | 4 + 8 | 12 | 3 |
| 3 | 4 + 8 + 12 | 24 | 6 |
| 4 | 4 + 8 + 12 + 16 | 40 | 10 |
| 5 | 4 + 8 + 12 + 16 + 20 | 60 | 15 |
| 6 | 4 + 8 + 12 + 16 + 20 + 24 | 84 | 21 |
| 7 | 4 + 8 + 12 + 16 + 20 + 24 + 28 | 112 | 28 |
| 8 | 4 + 8 + 12 + 16 + 20 + 24 + 28 + 32 | 144 | 36 |
| 9 | 4 + 8 + 12 + 16 + 20 + 24 + 28 + 32 + 36 | 180 | 45 |
| 10 | 4 + 8 + 12 + 16 +...+ 32 + 36 + 40 + 44 | 220 | 55 |
| www.osfantasticosnumerosprimos.com.br | |||
O produto de 4 pelo triangular 3 é igual a 12.
12 é a soma dos múltiplos 4 e 8.
12 é o quádruplo do triangular 3.
3 é o segundo número triangular.
As parcelas 4 e 8 se encontram na segunda linha da tabela.
O produto de 4 pelo triangular 6 é igual a 24.
24 é a soma dos múltiplos 4, 8 e 12.
24 é o quádruplo do triangular 6.
6 é o terceiro número triangular.
As parcelas 4, 8 e 12 se encontram na terceira linha da tabela.
O produto de 4 pelo triangular 10 é igual a 40.
40 é a soma dos múltiplos 4, 8, 12 e 16.
40 é o quádruplo do triangular 10.
10 é o quarto número triangular.
As parcelas 4, 8, 12 e 16 se encontram na terceira linha da tabela.
A Tabuada de Somas de Progressões Aritméticas demonstra de forma sintética as somas de progressões aritméticas cujos primeiros termos são dos números 2 a 10.
Querendo se saber por exemplo as somas de cada uma das sub-sequências dos múltiplos de 2 cujas quantidades de termos são de 1 a 10, veja a intersecção entre o número 2 e um número triangular.
| Tabuada de somas | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| de progressões aritméticas | |||||||||||
| quantidade de termos | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| números triangulares | |||||||||||
| x | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | 45 | 55 | |
| números | |||||||||||
| naturais | |||||||||||
| 2 | 2 | 6 | 12 | 20 | 30 | 42 | 56 | 72 | 90 | 110 | |
| 3 | 3 | 9 | 18 | 30 | 45 | 63 | 84 | 108 | 135 | 165 | |
| 4 | 4 | 12 | 24 | 40 | 60 | 84 | 112 | 144 | 180 | 220 | |
| 5 | 5 | 15 | 30 | 50 | 75 | 105 | 140 | 180 | 225 | 275 | |
| 6 | 6 | 18 | 36 | 60 | 90 | 126 | 168 | 216 | 270 | 330 | |
| 7 | 7 | 21 | 42 | 70 | 105 | 147 | 196 | 252 | 315 | 385 | |
| 8 | 8 | 24 | 48 | 80 | 120 | 168 | 224 | 288 | 360 | 440 | |
| 9 | 9 | 27 | 54 | 90 | 135 | 189 | 252 | 324 | 405 | 495 | |
| 10 | 10 | 30 | 60 | 100 | 150 | 210 | 280 | 360 | 450 | 550 | |
| www.osfantasticosnumerosprimos.com.br | |||||||||||
No livro digital Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs é apresentada nova fórmula exclusiva para saber a soma de n termos de múltiplos de um número natural.
Autor: Ricardo Silva - novembro/2020
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato