Página de estudos de matemática e sequências numéricas

Sequência de Fibonacci Semelhante (3-4) - 258

A Sequência de Fibonacci Semelhante (3-4), como outras da série, é assim denominada por possuir duas das principais propriedades da Sequência de Fibonacci:

1) cada termo são gerados pela soma de dois termos anteriores, a partir do terceiro termo;

2) o quociente de um termo pelo seu anterior é um número próximo ao Número phi (Ф), o Número de Ouro.

Os termos da Sequência de Fibonacci Semelhante (3-4) são gerados a partir dos números consecutivos 3 e 4.

A matéria:

011-estudos-257-sequencia-fibonacci-numeros-quadrados-parte-4

discorre de uma outra propriedade numérica da Sequência de Fibonacci de que um quadrado de um número de Fibonacci subtraído de um outro termo posterior de Fibonacci tem como resultado também um número quadrado perfeito.

Analisando a Sequência de Fibonacci Semelhante (3-4), verifica-se que ela também possui tal propriedade com algumas características apresentadas a seguir.

Diferença entre um termo ao quadrado e um outro termo da Sequência (3-4).

A diferença entre um termo ao quadrado e um outro termo posterior da Sequência (3-4) tem como resultado o número 2.

Os termos escolhidos se alternam, um sim e outro não.

Exemplos:

a) termo escolhido 3

Quadrado de 3 = 9

9 - 7 = 2

b) termo escolhido 7

Quadrado de 7 = 49

49 - 47 = 2

c) termo escolhido 18

Quadrado de 18 = 324

324 - 322 = 2

d) termo escolhido 47

Quadrado de 47 = 2209

2209 - 2207 = 2

Diferença entre um termo e um outro termo ao quadrado da Sequência (3-4)

A diferença entre um termo e um outro ao quadrado da Sequência (3-4) tem como resultado o número 2.

Os termos escolhidos se alternam, um sim e outro não.

Exemplos:

a) termo escolhido 4

Quadrado de 4 = 16

18 - 16 = 2

b) termo escolhido 11

Quadrado de 11 = 121

123 - 121 = 2

c) termo escolhido 29

Quadrado de 29 = 841

843 - 841 = 2

d) termo escolhido 76

Quadrado de 76 = 5776

5778 - 5776 = 2

Números compostos com quatro divisores

Diferentemente da Sequência de Fibonacci em que números primos tendem a aparecer na ordem ímpar, os da Sequência de Fibonacci Semelhante (3-4) aparecem tanto em ordem ímpar quanto par.

Os números destacados abaixo, apresentam características em comum, são ímpares, compostos e possuem 4 divisores.

Como se percebe, os intervalos entre eles não são constantes, isto é, são aleatórios, mas diferem de 2 unidades em relação algum termo anterior ao quadrado.

O terceiro termo dos divisores são números primos que em sua maioria terminam com algarismo 1.

Números compostos que possuem 4 divisores, são números que são produtos de dois números primos distintos e suas potências possuem divisores em quantidade de números quadrados perfeitos.

Números compostos cujas potências possuem divisores em quantidade de números quadrados perfeitos são os quais se podem construirem Quadrados Mágicos Multiplicativos Sequenciais.

Veja estudos publicados aqui no WeSite:

011-estudos-202-quadrados-magicos-multiplicativos-divisores-de-um-numero

011-estudos-203-quadrados-magicos-multiplicativos-e-divisores-de-36

011-estudos-204-quadrados-magicos-multiplicativos-e-divisores-de-100

Periodicidade da Sequência de Fibonacci Semelhante (3-4)

Joseph Louis Lagrange (1736-1813), matemático francês nascido da Itália, descobriu em 1774 que a periodicidade do algarismo da unidade de cada termo da Sequência de Fibonacci se repete em intervalos de 60 em 60 vezes, isto é, a cada grupo de 60 números, o último algarismo é o mesmo.

Na Sequência de Fibonacci Semelhante (3-4) também há esta propriedade de periodicidade.

A periodicidade do último algarismo de cada termo da sequência se apresenta da seguinte forma:

5 conjuntos de 8 termos (40 termos) terminados em:

3, 4, 7, 1, 8, 9, 7 6

5 conjuntos de 4 termos (20 termos) terminados em:

3, 9, 2, 1

Totalizando a mesma quantidade de 60 números da Sequência de Fibonacci.

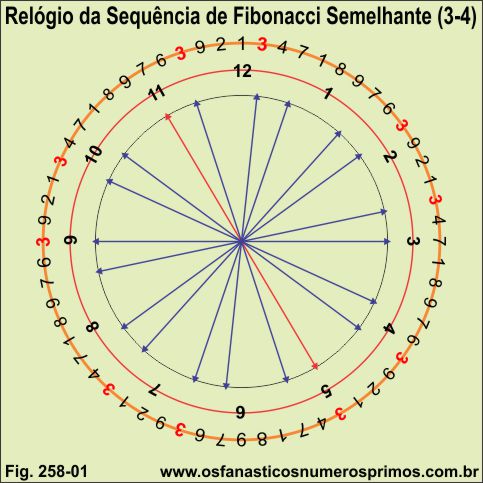
Dispondo os conjuntos de números em forma de um relógio, observa-se também regularidades numéricas.

Os números primos 3 e 7 aparecem diametralmente opostos.

A soma dos números oposto é sempre 10.

Os números primos opostos da sequência 3 e 7 aparecem alinhados com os números primos 5 e 11 do "relógio".

Observação: a verificação de números primos foram feitas através do WebSite Impérios dos Números

Autor: Ricardo Silva - maio /2020

Fontes Bibliográficas:

CARVALHO, Maria Cecília Costa e Silva. Padrões Numéricos e Sequências - São Paulo: Moderna, 1997

DIAS , Ricardo Alexandre da Rocha. Algumas evidências computacionais da infinitude dos números primos de Fibonacci e generalizações destes. Universidade Federal do Rio Grande do Norte Centro de Ciências Exatas e da Terra Departamento de Informática e Matemática Aplicada Curso de Ciências da Computação. Natal - RN, 2008.

FERREIRA, Rogério A. Seqüência de Fibonacci, UNIFIEO, São Paulo, v.01, p.14, 2006.

SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

Império dos números

The Fibonacci Association

Matérias relacionadas:

011-estudos-058-sequencia-fibonacci-numeros-quadrados-parte-1

011-estudos-069-ternos-pitagoricos

011-estudos-082-sequencia-fibonacci-numeros-quadrados-parte-2

011-estudos-083-sequencia-fibonacci-numeros-quadrados-parte-3

011-estudos-064-sequencia-fibonacci-figuras-geometricas-o-triangulo

011-estudos-065-sequencia-fibonacci-figuras-geometricas-o-quadrado

011-estudos-221-sequencia-fibonacci-e-regularidades-numericas

011-estudos-223-sequencia-fibonacci-e-ternos-pitagoricos

011-estudos-224-sequencia-lucas-e-ternos-pitagoricos

011-estudos-252-triangulos-fibonacci

011-estudos-253-tabuada-sequencia-fibonacci

011-estudos-254-sequencias-fibonacci-semelhantes

011-estudos-255-sequencias-fibonacci-semelhantes-numeros-primos

011-estudos-256-numeros-triangulares-e-diferenca-entre-quadrados-raizes

011-estudos-257-sequencia-fibonacci-numeros-quadrados-parte-4

Senhores Professores de Matemática,

Profissionais de Exatas e

Entusiastas Matemáticos

RECEBAM GRATUITAMENTE

O E-BOOK

TRIÂNGULO RETÂNGULO:

 

FAÇA A SUA SOLICITAÇÃO

AGORA MESMO ATRAVÉS

DO E-MAIL:

contato@osfantasticos numerosprimos.com.br

L A N Ç A M E N T O ! ! !

NOVO LIVRO DIGITAL:

DESCOBRINDO NÚMEROS PRIMOS A PARTIR DE NÚMEROS COMPOSTOS

NOVO LIVRO DIGITAL (E-book)

Mais informações, acesse:

SEÇÃO LIVROS

Prezado visitante, o conteúdo do

WebSite Os Fantásticos Números Primos

está protegido por direitos autorais.

O uso acadêmico e escolar está liberado,

desde que informando ao autor o local e

o meio em que será utilizado e divulgado,

através do e-mail:

contato@osfantasticosnumerosprimos.com.br

O uso comercial é proibido.