capa dos livros: os fantásticos números primos, sequências numéricas mágicas, estudos de sequências númericas, o triângulo retângulo

Página de estudos de matemática e sequências numéricas

Quadrados Mágicos 3x3 e métodos de construções - 198

O termo Quadrado Mágico, até hoje não se sabe quem o cunhou, mas pelos relatos e lendas chinesas de que tenha aparecido inscrito no casco de uma tartaruga símbolos que representavam quantidades e que quando somados resultavam 15, passou a ter um carater místico e sobrenatural associado a longevidade da tartaruga por ser um animal venerado, a este diagrama em forma de quadrado os chineses o chamaram de Lo-shu.

Quadrados Mágicos são dispositivos formados por matrizes quadriculadas nos quais números são dispostos em linhas e colunas em certa ordem de forma que a soma de cada linha, cada coluna, bem como as diagonais apresentam sempre a mesma soma a qual é denominada de Constante Mágica.

Quadrados Mágicos são classificados conforme a sua ordem, isto é, quadrados de ordem 3 (3x3) são formados por 3 linhas e 3 colunas, perfazendo um total de 9 células, de ordem 4 (4x4) é formando por 16 células, de ordem 5 (5x5) é formado por 25 células e assim por diante.

Os estudos aqui apresentados faz comparações entre os Método Yang Hui "Pirâmide, Método da Rotação e Método La Loubère e apontam curiosidades e semelhanças nas construções de quadrados mágicos de ordem ímpar, isto é, quadrados cujas quantidade de células são ímpares.

Observação importante:

a) Quadrados Mágicos 3x3 cujas progressões aritméticas iniciam-se em número ímpar, as diagonais são constituídas por números pares;

b) Quadrados Mágicos 3x3 cujas progressões artméticas iniciam-se em número par, as diagonais são constituídas por números ímpares.

Quadrados Mágicos 3x3 imperfeitos

Quadrados Mágicos Imperfeitos são quadrados que não apresentam Constante Mágica em todas linhas, colunas e diagonais.

Quadrados Mágicos Imperfeitos podem ser construídos naturalmente por sequências numéricas consecutivas de 1 a n² dispostas em matrizes quadriculadas.

O Quadrado Mágico 3x3 Imperfeito formado pela progressão aritimética de 1 a 9 possui as seguintes características:

Quadrado a)

1) as diagonais tem como resultado a Constante Mágica 15;

2) a linha e coluna centrais tem como resultado a Constante Mágica 15;

3) as somas são múltiplos de 3;

4) o termo médio 5 se encontra na célula central do quadrado;

Observação: mesmo sendo um Quadrado Mágico Imperfeito ele possui também Constante Mágica aparecendo nas diagonais, linha e coluna centrais.

Quadrados 3x3, 4x4, 5x5, etc, de números consecutivos são bases de estudos publicados no livro Sequências Numéricas Magicas [1] sobre relações numéricas entre figuras geométricas, números figurados, números naturais, números quadrados perfeitos , números cúbicos, etc.

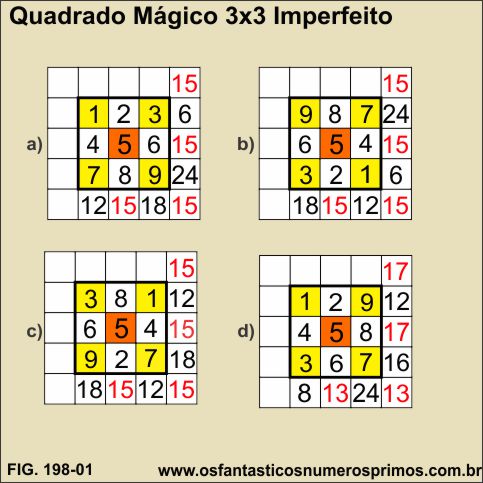
Será que é possível, manter sempre o número 5 na célula central, mudar os outros números das células dos extremos nas diagonais e nas linhas, mas sem mudá-los de diagonais e linhas.

Quadrado b)

Trocando de posição os números dos extremos, o quadrado permanece Imperfeito, mas mantem a Constante Mágica nas diagonais e linha centrais.

Quadrado c)

Trocando de posição os números dos extremos, o quadrado permanece Imperfeito, mas mantem a Constante Mágica nas diagonais e linha centrais.

Quadrado d)

Trocando de posição os números dos extremos e o pares de números correspondentes, o quadrado permanece Imperfeito, sem manter a Constante Mágica nas diagonais e linha centrais.

Mantendo-se números ímpares nos extremos da diagonais e trocando tanto ímpares e pares de células não é possível montar um Quadrado Mágico Puro.

Quadrado Mágico 3x3 e o Método de Construção Yang Hui "Pirâmide"

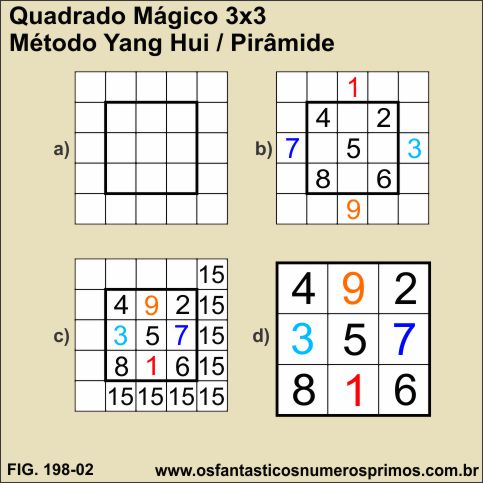
O Método Yang Hui ou "Pirâmide" consiste em:

a) fazer um quadriculado base maior e centralizar o quadrado 3x3;

b) numerar diagonalmente a partir parte superior da coluna central;

Obervação: números pares ficam dentro do quadrado 3x3 e os ímpares ficam de fora.

c) os números devem ser trocados de posições:

número 1 que estava na parte superior, deve ficar na parte inferior do quadrado;

o 9 deve ficar na parte superior do quadrado;

o 3 deve ficar na lateral esquerda do quadrado;

e o 7 na lateral direita do quadrado.

d) Temos um configuração completamente diferente em relação ao quadrado de números consecutivos:

Os números ímpares agora estão em linhas horizontal e vertical;

Os números pares agora se encontram nas diagonais;

O número 5 permanece em sua posição central;

A partir desta configuração é possível formar outros 7 Quadrados Mágicos 3x3 por meio de reflexão e rotação de seus elementos.

quadrado mágico 3x3 - método yanh hu - pirâmide

Quadrados Mágicos 3x3 e os Métodos de Rotação e de Yang Hui "Pirâmide" e La Loubère

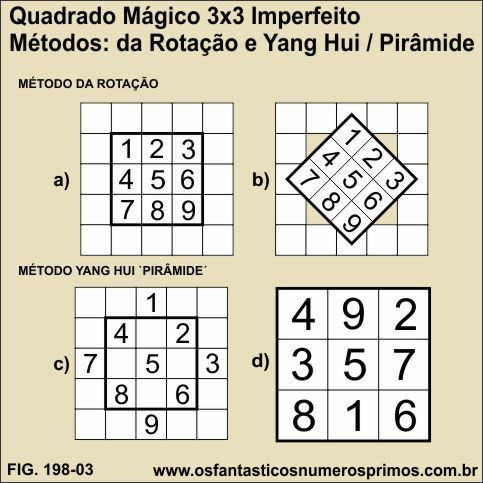
a) contruir um quadrado base e um Quadrado Mágico Imperfeito 3x3 com números de 1 a 9;

b) rotacionando o quadrado 3x3 de números consecutivos a 90⁰, os números ímpares se posicionam na linha e coluna centrais e os pares na diagonais;

Veja mais detalhes do Método de Rotação aqui no WebSite: 011-estudos-170-quadrados-magicos-ordem-3.

Como se poder observar, o Método Yang Hui / "Pirâmide" tem em sua essência a rotação do termos de um quadrado de ordem ímpar.

quadrados mágicos 3x3 e métodos de Rotação e Yang Hui - Pirâmide-

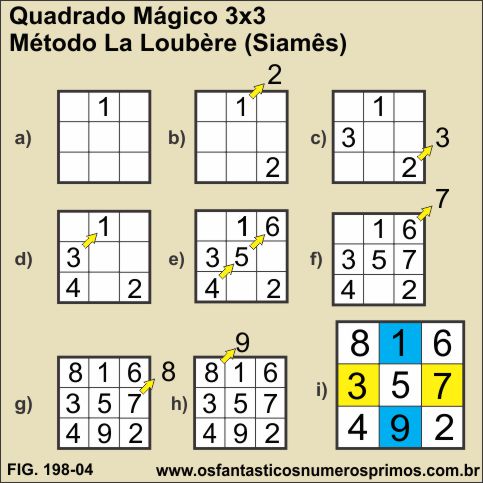
No Método La Loubere, os números também são rotacionados, de forma que os ímpares ficam nas linha e coluna centrais e os pares nas diagonais (figura 198-04, detalhe i).

Há uma reflexão dos termos do quadrados em relação aos outros métodos descrito acima.

Veja mais detalhes do Método de La Loubère aqui no WebSite: 011-estudos-170-quadrados-magicos-ordem-3.

quadrados magicos 3x3 - método la loubere

Quadrados Mágicos 3x3 e o Método de Construção De La Hire

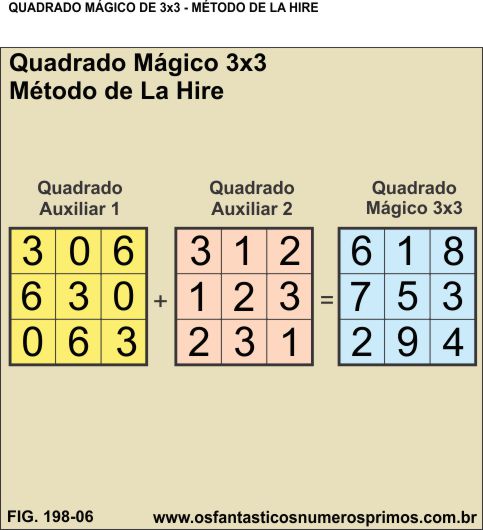
O método de construção de Quadrados Mágicos 3x3 De La Hire [3] consiste em construir dois quadrados auxiliares e posteriormente somar os termos correspondentes das duas sequências numéricas.

A primeira sequência é formada pelos 3 primeiros múltiplos de 3.

m(3) = {0, 3, 6}

A segunda sequência é formada pela quantidade de células (linha ou coluna) do quadrado: 1, 2, 3.

1) Primeiro quadrado auxiliar

a) coloca-se o termo central (3) dos múltiplos de 3 na diagonal principal, da esquerda superior para a direita inferior;

b) em qualquer ordem, preenche-se a primeira linha do quadrado com os demais múltiplos (neste exemplo foram dispostos em ordem crescente: 0 e 6;

c) preenche-a diagonal quebrada seguindo a ordem da primeira linha, da esquerda superior para a direita inferior, repetindo-se neste caso o 0 (zero);

d) preenche-a diagonal quebrada inferior, da esquerda superior para a direita inferior, repetindo-se neste caso o 6 (seis);

e) preenche-a diagonal quebrada final, da esquerda superior para a direita inferior, repetindo-se neste caso o 0 (zero);

f) na montagem final do primeiro quadrado auxiliar, os números ficam dispostos nas células de forma que não se repetem em cada linha e em cada coluna.

2) Segundo quadrado auxiliar

g) preenche-se com o termo central (2) a diagonal secundária, da direita superior para a esquera inferior;

h) em qualquer ordem preenche-se a primeira linha do quadrado com os demais números (neste exemplo foram dispostos em ordem crescente: 1 e 3;

i) preenche-a diagonal quebrada superior seguindo a ordem da primeira linha, da direita superior para a esquerda inferior, repetindo-se neste caso o 1 (um);

j) preenche-a diagonal quebrada inferior, da direita superior para a esquerda inferior, repetindo-se neste caso o 3 (três);

k) preenche-a diagonal quebrada final, da direita superior para a esquerda inferior, repetindo-se neste caso o 1 (um);

l) na montagem final do segundo quadrado auxiliar, os números ficam dispostos nas células de forma que não se repetem em cada linha e em cada coluna.

3) Construção do Quadrado Mágico 3x3 com método De La Hire

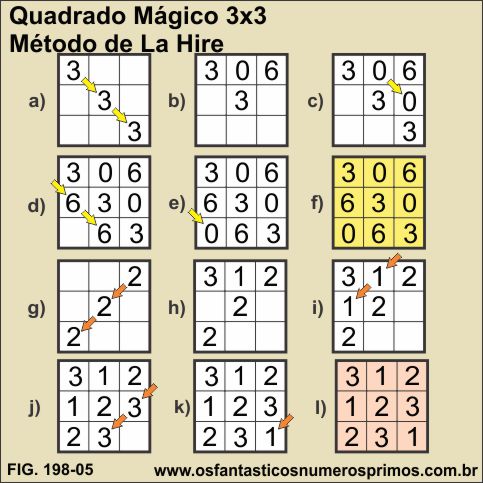
Após montagens dos quadrados auxiliares, somam-se os termos correspondentes, obtendo-se assim o Quadrado Mágico 3x3 com a sequência dos 9 primeiros números naturais.