Página de estudos de matemática e sequências numéricas

Quadrados Mágicos 8x8 - 195

Quadrado Mágico 8x8 ou de ordem 8 é um quadrado quadriculado formado por 8 linhas e 8 colunas perfazendo um total de 64 células.

O Quadrado Mágico de ordem 8 Normal ou Puro tem como formação os 64 primeiros números naturais (1, 2, 3, 4, 5, 6, 7, 8, 9, 10 , ... , 60 , 61, 62, 53 e 64) ou 1 a n² com Costante Mágica 260 e soma de todos os números 2.080.

Quadrado Mágico 8x8 e o Método de Moschopoulos

O Método de Manuel Moschopoulos, autor bizantino que escreveu um tratado matemático sobre quadrados mágicos baseado nos textos de Ahmed al-Buni [1], também chamado de Método Igualmente Uniforme funciona para quadrados mágicos de ordem par múltiplos de 4 (4, 8, 16, 32, 64, ...).

A técnica de construção se baseia na configuração de Quadrado Mágico de ordem 4 com algumas particularidades.

É uma técnica bastante simples em que consiste de alguns passos:

a) contruir um quadrado de 64 células;

b) dividir em 4 sub-quadrados de 16 células;

c) marcar as diagonais do quadrado maior e dos sub-quadrados;

d) preencher com os números de 1 a 64 as células com fundo branco, saltado as células que estão em sentidos diagonais (células amarela);

e) o quadrado maior de 64 células segue o esquema de montagem do quadrado 4x4;

f) o primeiro preechimento com números deve ficar igual a figura 195-01;

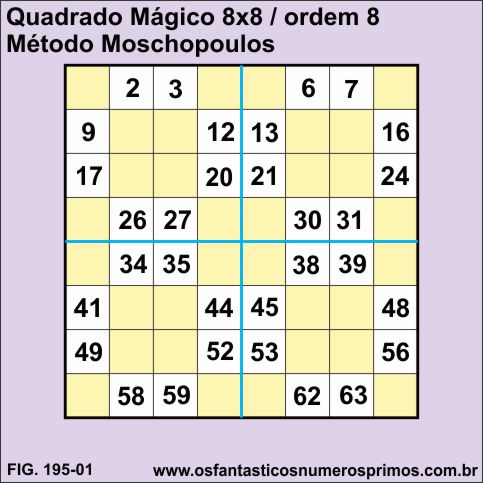
d) posteriormente, preenchem-se as células amarela, começando da parte inferior direita, preenchendo cada linha e subindo;

e) o quadrado mágico deve ficar igual o da figura 195-02.

Quadrado Mágico 8x8 e soma mágica 260

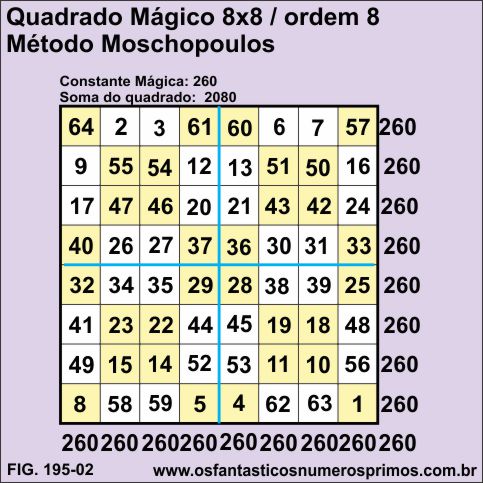
O Quadrado Mágico de ordem 8 formado com o Método de Moschopoulos tem como Constante Mágica 260 e a soma de todos os seus termos 2.080 e apresenta as seguintes propriedades numéricas adicionais:

a) quaisquer sub-quadrados de 2 x 2 tem como resultado 130 que é a metade da Constante Mágica;

b) quaisquer sub-quadrados de 4 x 4 tem como resultado 520 que é o dobro da Constante Mágica;

c) os cantos do quadrado principal e dos sub-quadrados tem como resultado 130 que é metade da Constante Mágica;

d) formando um "octógono" maior a soma dos números tem como resultado 520, o dobro da Costante Mágica;

d) formando um "octógono" menor a soma dos números tem como resultado 130, a metade da Costante Mágica;

Permutação dos sub-quadrados 4x4 (16 células)

Os sub-quadrados 4x4 tem a soma de todos os seus números 520, que é o dobro da Constante Mágica e a metade da soma de todos os números do quadrado 8x8 (64 células).

Permutando os sub-quadrados, a Constante Mágica e a soma de todos os números do Quadrado Mágico de ordem 8 não se alteram.

Veja alguns exemplos, mantendo-se fixo o sub-quadrado de fundo amarelo.

a)

b)

c)

d)

e)

f)

Quadrado Mágico 8x8 e números quadrados perfeitos

Elevando-se os números de 1 a 64 do Quadrado Mágico de ordem 8 ao quadrado, obtem-se um Quadrado Mágico Imperfeito com as sequintes características:

Somas das linhas

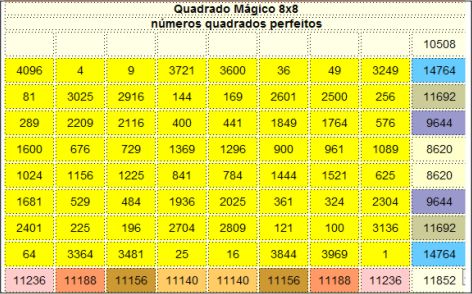
a) a soma dos números quadrados perfeitos da primeira linha é igual a soma dos quadrados da oitava linha;

b) a soma dos números quadrados perfeitos da segunda linha é igual a soma dos quadrados da sétima linha;

c) a soma dos números quadrados perfeitos da terceira linha é igual a soma dos quadrados da sexta linha;

d) a soma dos números quadrados perfeitos da quarta linha é igual a soma dos quadrados da quinta linha;

Somas das colunas

e) a soma dos números quadrados perfeitos da primeira coluna é igual a soma dos quadrados da oita coluna;

f) a soma dos números quadrados perfeitos da segunda coluna é igual a soma dos quadrados da sétima coluna.

g) a soma dos números quadrados perfeitos da terceira coluna é igual a soma dos quadrados da sexta coluna.

h) a soma dos números quadrados perfeitos da quarta coluna é igual a soma dos quadrados da quinta coluna.

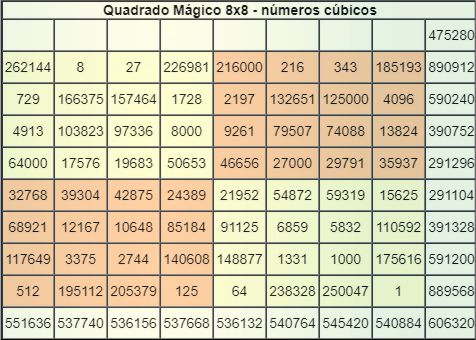
i) a soma dos números de cada sub-quadrados 4x4 na diagonal principal (cor amarela) têm os mesmos resultados 23.384;

j) a soma dos números de cada sub-quadrados 4x4 na diagonal secundária (cor laranja) têm os mesmos resultados 21.336;

Quadrado Mágico 8x8 e números cúbicos

Elevando-se os números de 1 a 64 do Quadrado Mágico de ordem 8 ao cubo, obtem-se um Quadrado Mágico Imperfeito com as sequintes características:

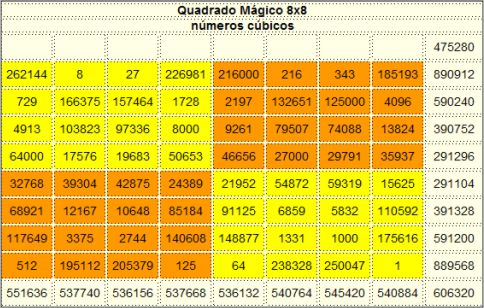
a) a soma dos números de cada sub-quadrados 4x4 na diagonal principal (cor amarela) têm os mesmos resultados 1.181.440;

b) a soma dos números de cada sub-quadrados 4x4 na diagonal secundária (cor laranja) têm os mesmos resultados 981.760;

c) as somas de cada uma da linhas, bem como as colunas apresentam resultados diferentes.

O quadrado 8x8 e números consecutivos

No livro Sequências Numéricas Magicas [2] estão publicados vários estudos sobre relações numéricas entre figuras geométricas, números figurados, naturais, quadrados, cúbicos, etc.

Em um desses estudos, os 64 primeiros números naturais são dispostos sequencialmente dentro de um quadrado 8x8 apresentando entre outras, as seguintes propriedadas numéricas:

a) as diagonais têm como resultados a Constante Mágica 260;

b) a soma de cada uma das linha horizontais não é múltiplo de 8;

c) a soma de cada uma das colunas têm como resultados múltiplos de 8;

d) a soma de todos os números do quadrado tem como resultado a Soma Mágica 2080.

Quadrado Mágico 8x8 e o Método Troca de Diagonal

Este método também permite construir quadrados mágicos múltiplos de 4 (8, 16, 32,...), marcando-se as diagonais através de sub-quadrados [3].

Para construir Quadrado Mágico de ordem 8 devemos:

a) dividir o quadrado de 8x8 células em 4 quadrantes, isto é, em 4 sub-quadrados de 4x4 células (linhas azul);

b) tendo como referência o primeiro quadrante, marcar as células da diagonal secudária (células amarela);

c) marcar a diagonal quebrada (células laranja);

d) marcar uma célula da diagonal principal (célula verde);

e) o primeiro quadrante se refetle à direita e a baixo, formando um "octógono";

f) numerar a células coloridas conforme a sua ordem, começando da parte superior esquerda, deixando as células brancas vazias;

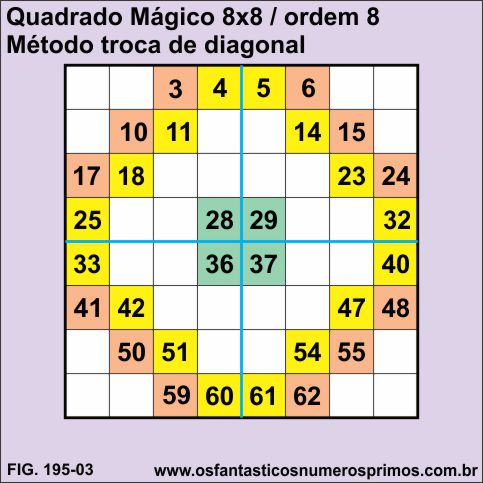
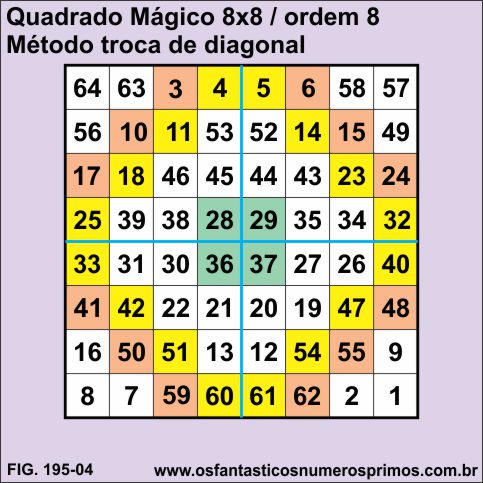
g) para finalizar, a partir da parte inferior direita, numere as células branca começando pelo número 1, contando as células coloridas, mas pulando-as.

Com esta variante de construção, obtem-se também um Quadrado Mágico de ordem 8, com Constante Mágica 260.

Autor: Ricardo Silva julho/2018

Fontes Bibliográficas:

[1] https://www.maa.org/press/ periodicals/convergence/ the-magic-squares-of-manuel-moschopoulos-the-mathematics-of-the-methods-evenly-even-squares

[2] SILVA, Ricardo José da. Sequências Numéricas Mágicas. São Paulo, livro digital, 2013

[3] SANTOS, Rubiana Feliciano da Costa - Monografia: Quadrados Mágicos. Universidade Federal de Goiás - UFG - Departamente de Matemática - DM. Catalão - Goiás - 2018.

SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

Matérias relacionadas:

011-estudos-169-quadrados-magicos

011-estudos-170-quadrados-magicos-ordem-3

011-estudos-171-quadrados-magicos-pitagoricos

011-estudos-172-quadrados-magicos-numeros-primos

011-estudos-173-quadrado-magico-ordem3-numero-30

011-estudos-174-quadrados-magicos-numeros-quadrados-perfeitos

011-estudos-175-quadrados-magicos-pitagoricos-e-os-numeros-3-4-5

011-estudos-176-quadrados-magicos-e-qualquer-numero

011-estudos-177-ternos-pitagoricos-e-formula-de-euclides

011-estudos-180-quadrados-magicos-bimagicos-multimagicos

011-estudos-181-quadrados-magicos-ordem3-4-5-e-numeros-quadrado-perfeitos

011-estudos-182-quadrados-magicos-pitagoricos-de-ordem-3-3-3

011-estudos-183-quadrados-magicos-pitagoricos-3-3-3-imperfeito

011-estudos-184-quadrados-magicos-ordem-4

011-estudos-185-quadrados-magicos-ordem-4-numeros-quadrados-perfeitos

011-estudos-186-quadrados-magicos-ordem-5

011-estudos-187-quadrados-magicos-de-ordem5-numeros-quadrados-perfeitos

011-estudos-188-quadrados-magicos-pitagoricos-ordem-5-5-5

011-estudos-189-circulo-magico-benjamin-franklin-desvendado

011-estudos-190-quadrados-antimagicos-ordem-3

NOVO LIVRO DIGITAL (E-book)

Mais informações, acesse:

SEÇÃO LIVROS

Manual Digital (E-book) Quadrado Mágico Triplo

DOWNLOAD GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Livro Ternos Pitagóricos e sequências numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Prezado visitante, o conteúdo do

WebSite Os Fantásticos Números Primos

está protegido por direitos autorais.

O uso acadêmico e escolar está liberado,

desde que informando ao autor o local e

o meio em que será utilizado e divulgado,

através do e-mail:

contato@osfantasticosnumerosprimos.com.br

O uso comercial é proibido.