


Quadrados Mágicos tem sua origem na antiga China, em seus primórdios foram utilizados como algo sobrenatural, isto é, como uma divindade associada a deuses, e com o tempo, outras civilizações tomaram conhecimento desse dispositivo numérico o qual também utilizavam como um objeto místico, relacionando-os aos planetas do sistema solar, mapas astrológicos, amuletos contra pestes e doenças.
Manuel Moschopoulos, escritor bizantino, traduziu manuscritos árabes e gregos para o latim, e entre eles, o texto de Ahmed al-Buni do século XIII, que discorria sobre as propriedades místicas de quadrados mágicos, tradução esta que fora encontrada por Fhelipe de la Hire na Biblioteca de Paris.
O crédito dado a Manuel Moschopoulos é que ele escreveu um tratado sobre quadrados mágicos focando nas caractéristicas matemáticas, desvinculando-os de caráter místico e sobrenatural.
Quadrados Mágicos Imperfeitos são os que nas somas de cada linha, cada coluna e diagonais apresentam resultados diferentes uns dos outros, as vezes números consecutivos, as vezes duas linhas ou colunas com somas iguas, etc.
Aqui são apresentados exemplos de Quadrados Mágicos Imperfeitos 5x5, mas se colocando na posição daqueles estudiosos e entusiastas que passaram horas e horas tentado criar técnicas e algoritimos precisos para se tornar Método de Construção de Quadrados Mágicos.
Quadrados formados por números consecutivos e dispostos sequencialmente linha por linha formam Quadrados Mágicos Imperfeitos, isto porque, nem todas as somas das linhas horizontais e verticais têm como resultado Constante Mágica.
No livro Sequências Numéricas Magicas [1] estão publicados vários estudos sobre relações numéricas entre figuras geométricas, números figurados, naturais, quadrados, cúbicos, etc.
Em um desses estudos, os 25 primeiros números naturais são dispostos sequencialmente dentro de um quadrado 5x5 (25 células) apresentando várias propriedades numéricas:
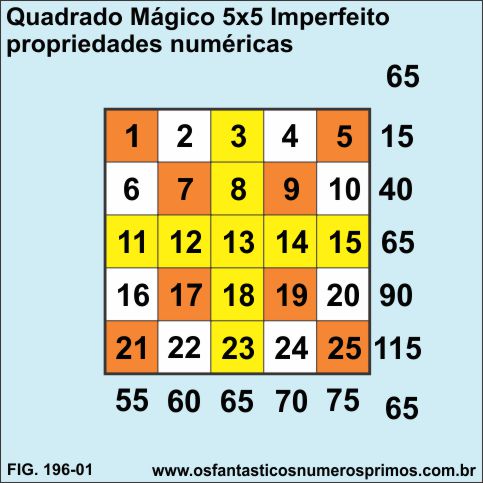
a) as diagonais (cor laranja) têm como resultado a Constante Mágica 65;
b) as linhas e colunas centrais (cor amarela) têm como resultado a Constante Mágica 65;
b) a soma de cada linha horizontal é múltiplo de 5;
c) a soma de cada linha vertical é múltiplo de 5;
d) a soma de todos os números do quadrado tem como resultado 325.
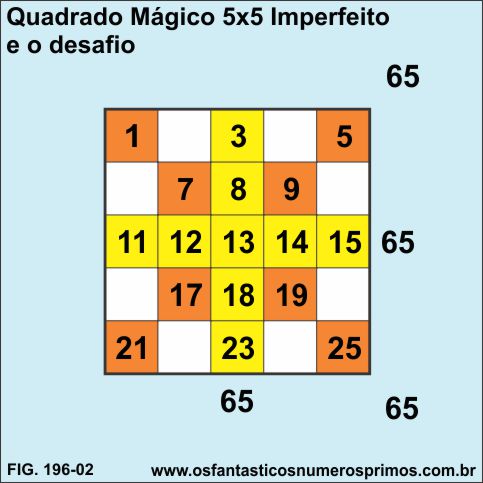
Deixo aqui um desafio, a você visitante!
Será que é possível mover SOMENTE os números (2, 4, 6, 10, 16, 20, 22 e 24) que estão nas células brancas de um lugar para outro para se formar um Quadrado Mágico?
Veja que as diagonais e as linhas centrais já têm como resultados a Constante Mágica 65.
As demais linhas e colunas, ou estão com somas menores ou com as somas maiores que 65.
Exemplo 1)
Os números partem do centro formando espiral, exemplo de construção baseado na espiral do matemático Stanislaw Ulam.
A soma de cada uma das colunas, linhas e diagonais são diferentes.
| Quadrado Mágico 5x5 | ||||||
| constante mágica 45 | ||||||
| 45 | ||||||
| 17 | 16 | 15 | 14 | 13 | 75 | |
| 18 | 5 | 4 | 3 | 12 | 42 | |
| 19 | 6 | 1 | 2 | 11 | 39 | |
| 20 | 7 | 8 | 9 | 10 | 54 | |
| 21 | 22 | 23 | 24 | 25 | 115 | |
| 95 | 56 | 51 | 52 | 71 | 57 | |
Exemplo 2)
Os números são posicionados diagonalmente.
Pares de colunas e linhas apresentam resultados iguais.
| 85 | ||||||
| 1 | 6 | 14 | 20 | 24 | 65 | |
| 10 | 2 | 7 | 15 | 21 | 55 | |
| 17 | 11 | 3 | 8 | 16 | 55 | |
| 22 | 18 | 12 | 4 | 9 | 65 | |
| 25 | 23 | 19 | 13 | 5 | 85 | |
| 75 | 60 | 55 | 60 | 75 | 15 |
Exemplo 3)
Os números são posicionados diagonalmente dois a dois nos extremos.
A soma de cada uma das colunas, linhas e diagonais são diferentes.
| 45 | ||||||
| 0 | ||||||
| 1 | 9 | 13 | 11 | 4 | 38 | |
| 17 | 6 | 19 | 8 | 16 | 66 | |
| 21 | 22 | 23 | 24 | 25 | 115 | |
| 15 | 7 | 20 | 5 | 18 | 65 | |
| 3 | 12 | 14 | 10 | 2 | 41 | |
| 0 | ||||||
| 57 | 56 | 89 | 58 | 65 | 37 |
Exemplo 4)
Os números são posicionados nos extremos preenchendo as diagonais e pares de colunas têm soma iguais.
Pares de colunas e linhas apresentam resultados iguais.
| 45 | ||||||
| 21 | 13 | 7 | 3 | 1 | 45 | |
| 17 | 22 | 14 | 8 | 4 | 65 | |
| 10 | 18 | 23 | 15 | 9 | 75 | |
| 5 | 11 | 19 | 24 | 16 | 75 | |
| 2 | 6 | 12 | 20 | 25 | 65 | |
| 55 | 70 | 75 | 70 | 55 | 115 |
Exemplo 5)
Os números são posicionados nos extremos, "circulando" o quadrado de fora para dentro.
A soma de cada uma das colunas, linhas e diagonais são diferentes.
| 86 | ||||||
| 9 | 5 | 1 | 16 | 12 | 43 | |
| 13 | 17 | 22 | 19 | 8 | 79 | |
| 2 | 23 | 25 | 21 | 4 | 75 | |
| 6 | 20 | 24 | 18 | 15 | 83 | |
| 10 | 14 | 3 | 7 | 11 | 45 | |
| 40 | 79 | 75 | 81 | 50 | 80 |
Exemplo 6)
Os números são posicionados diagonalmente e pares de colunas apresentam resultados iguais.
| 69 | ||||||
| 11 | 16 | 1 | 7 | 24 | 59 | |
| 20 | 12 | 17 | 2 | 8 | 59 | |
| 4 | 21 | 13 | 18 | 3 | 59 | |
| 9 | 5 | 22 | 14 | 19 | 69 | |
| 25 | 10 | 6 | 23 | 15 | 79 | |
| 69 | 64 | 59 | 64 | 69 | 65 |
Exemplo 7)
Os números são posicionados em ordem resersa e as somas das colunas são números consecutivos.
As diagonais tem como resultado a Constante Mágica 65.
| 65 | ||||||
| 1 | 2 | 3 | 4 | 5 | 15 | |
| 15 | 14 | 13 | 12 | 11 | 65 | |
| 21 | 22 | 23 | 24 | 25 | 115 | |
| 20 | 19 | 18 | 17 | 16 | 90 | |
| 6 | 7 | 8 | 9 | 10 | 40 | |
| 63 | 64 | 65 | 66 | 67 | 65 |
Exemplo 8)
A diagonal principal é formada por números consecutivos (semelhante aos Métodos Yang Hui/Pirâmide e Simom de La Loubère, demais números em ordem reversa.
| 68 | ||||||
| 11 | 1 | 2 | 3 | 4 | 21 | |
| 8 | 12 | 7 | 6 | 5 | 38 | |
| 17 | 16 | 13 | 10 | 9 | 65 | |
| 21 | 20 | 19 | 14 | 18 | 92 | |
| 25 | 24 | 23 | 22 | 15 | 109 | |
| 82 | 73 | 64 | 55 | 51 | 65 |
Exemplo 9)
A diagonal principal é formada pelos números consecutivos de 11 a 15 (semelhante aos Métodos Yang Hui/Pirâmide e Simom de La Loubère).
Primero são posicionados os números ímpares e depois só os pares.
As somas das colunas são números consecutivos.
As diagonais tem como resultado a Constante Mágica 65.
| 65 | ||||||
| 0 | ||||||
| 11 | 1 | 3 | 5 | 7 | 27 | |
| 9 | 12 | 17 | 19 | 21 | 78 | |
| 23 | 25 | 13 | 2 | 4 | 67 | |
| 6 | 8 | 10 | 14 | 16 | 54 | |
| 18 | 20 | 22 | 24 | 15 | 99 | |
| 0 | ||||||
| 67 | 66 | 65 | 64 | 63 | 65 |
Exemplo 10)
A diagonal principal é formada pelos números consecutivos 11 a 15 (semelhante aos Métodos Yang Hui/Pirâmide e Simom de La Loubère).
Primero são posicionados os números ímpares e depois só os pares em ordem reversas.
As diagonais tem como resultado a Constante Mágica 65.
| 65 | ||||||
| 11 | 25 | 23 | 21 | 19 | 99 | |
| 17 | 12 | 9 | 7 | 5 | 50 | |
| 3 | 1 | 13 | 24 | 22 | 63 | |
| 20 | 18 | 16 | 14 | 10 | 78 | |
| 8 | 6 | 4 | 2 | 15 | 35 | |
| 59 | 62 | 65 | 68 | 71 | 65 |
Autor: Ricardo Silva - julho/2018
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
[1] SILVA, Ricardo José da. Sequências Numéricas Mágicas. São Paulo, livro digital, 2013
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato